Question

If the angle $\angle A={{90}^{\circ }}$ in the $\Delta ABC$, then \[{{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right)\] is
A. 0
B. 1
C. $\dfrac{\pi }{4}$
D. $\dfrac{\pi }{6}$
E. $\dfrac{\pi }{8}$

Answer 1

Hint: We first use the triangle formula of the angles and then the trigonometric additional form of \[{{\tan }^{-1}}x+{{\tan }^{-1}}y={{\tan }^{-1}}\dfrac{x+y}{1-xy}\]. We also use Pythagoras’ theorem ${{b}^{2}}+{{c}^{2}}={{a}^{2}}$. We put the values of \[x=\left( \dfrac{c}{a+b} \right),y=\left( \dfrac{b}{a+c} \right)\] and find the particular solution for the inverse.

Complete step-by-step solution:
In $\Delta ABC$, we get $\angle A={{90}^{\circ }}$. Therefore, $\Delta ABC$ is a right-angle triangle whose hypotenuse is the opposite side of the angle $\angle A={{90}^{\circ }}$.

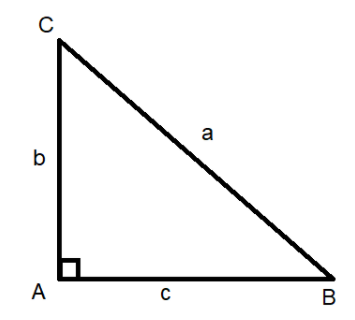
From Pythagoras’ theorem we know that ${{b}^{2}}+{{c}^{2}}={{a}^{2}}$.
We now use the trigonometric additional form of \[{{\tan }^{-1}}x+{{\tan }^{-1}}y={{\tan }^{-1}}\dfrac{x+y}{1-xy}\].
Now we place \[x=\left( \dfrac{c}{a+b} \right),y=\left( \dfrac{b}{a+c} \right)\].
We get \[{{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right)={{\tan }^{-1}}\left( \dfrac{\dfrac{c}{a+b}+\dfrac{b}{a+c}}{1-\dfrac{c}{a+b}\times \dfrac{b}{a+c}} \right)\].
We multiply with \[\left( a+c \right)\left( a+b \right)\] and get
\[\begin{align}
  & {{\tan }^{-1}}\left( \dfrac{\dfrac{c}{a+b}+\dfrac{b}{a+c}}{1-\dfrac{c}{a+b}\times \dfrac{b}{a+c}} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{c\left( a+c \right)+b\left( a+b \right)}{\left( a+c \right)\left( a+b \right)-bc} \right) \\
\end{align}\]
We simplify the equation and get
\[\begin{align}
  & {{\tan }^{-1}}\left( \dfrac{c\left( a+c \right)+b\left( a+b \right)}{\left( a+c \right)\left( a+b \right)-bc} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{ac+{{c}^{2}}+{{b}^{2}}+ab}{{{a}^{2}}+ab+ac+bc-bc} \right) \\
\end{align}\]
We replace the values ${{b}^{2}}+{{c}^{2}}={{a}^{2}}$ in the equation.
\[\begin{align}
  & {{\tan }^{-1}}\left( \dfrac{ac+{{c}^{2}}+{{b}^{2}}+ab}{{{a}^{2}}+ab+ac+bc-bc} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{ac+{{a}^{2}}+ab}{ac+{{a}^{2}}+ab} \right) \\
 & ={{\tan }^{-1}}1 \\
\end{align}\]
Now as the angle is an angle of a triangle, we can find the particular solution of the inverse.
So, \[{{\tan }^{-1}}\left( \dfrac{c}{a+b} \right)+{{\tan }^{-1}}\left( \dfrac{b}{a+c} \right)={{\tan }^{-1}}1=\dfrac{\pi }{4}\].
Therefore, the correct option is C.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\infty \le x\le \infty $. In that case we have to use the formula $x=n\dfrac{\pi }{2}+a$ for $\tan \left( x \right)=\tan a$ where $-\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2}$. For our given problem \[{{\tan }^{-1}}1=\dfrac{\pi }{4}\], the general solution will be $x=n\dfrac{\pi }{2}+\dfrac{\pi }{4}$. Here $n\in \mathbb{Z}$. But for $\Delta ABC$, we get $\angle A={{90}^{\circ }}$. So, other angles are acute.