Question

If the altitude of an equilateral triangle is $\sqrt{6}cm$. Find its area?
(a) $2\sqrt{3}c{{m}^{2}}$
(b) $2\sqrt{2}c{{m}^{2}}$
(c) $3\sqrt{3}c{{m}^{2}}$
(d) $6\sqrt{2}c{{m}^{2}}$

Answer 1

Hint: First of all draw the equilateral triangle with altitude as $\sqrt{6}cm$.We know that altitude makes ${{90}^{\circ }}$ on the base of the triangle and all the internal angles of the equilateral triangle are of ${{60}^{\circ }}$ so using trigonometric ratios we can find the side of the triangle. Then the area of the triangle is equal to $\dfrac{1}{2}\left( base \right)\left( altitude \right)$. Substitute base as the side of the triangle and altitude is given. Hence, we have calculated the area of the triangle.

Complete step-by-step answer:
In the below diagram, we have drawn an equilateral triangle with side length “a” and altitude of length $\sqrt{6}cm$
  

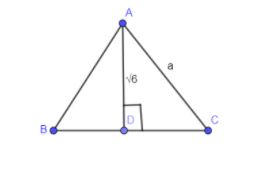
We know that all the internal sides of the equilateral triangle are equal with a measure of ${{60}^{\circ }}$. In the below figure, we have modified the above figure by adding the angle ${{60}^{\circ }}$ to it.
 

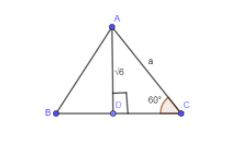
As you can see that $\Delta ADC$ is a right angled triangle so we can apply trigonometric ratios to it to get the value of “a”.
In the above diagram, AC (or “a”) is the hypotenuse of $\Delta ADC$ and AD is the perpendicular with respect to angle ${{60}^{\circ }}$ so we can use $\sin {{60}^{\circ }}$ to get the value of “a”.
$\sin {{60}^{\circ }}=\dfrac{Perpendicular}{Hypotenuse}$
Substituting perpendicular as AD and hypotenuse as AC in the above equation we get,
$\sin {{60}^{\circ }}=\dfrac{AD}{AC}$
Substituting AD as $\sqrt{6}$ and AC as “a” in the above equation we get,
$\sin {{60}^{\circ }}=\dfrac{\sqrt{6}}{a}$
From the trigonometric ratios, the value of $\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$ so using this value in the above equation we get,
$\begin{align}
  & \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{6}}{a} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}\left( \sqrt{2} \right)}{a} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{\left( \sqrt{2} \right)}{a} \\
\end{align}$
Cross multiplying the above equation we get,
$a=2\sqrt{2}cm$
Hence, we have got the length of the side of the equilateral triangle as $2\sqrt{2}cm$.
We know that area of the triangle is equal to:
$\dfrac{1}{2}\left( base \right)\left( altitude \right)$
Since base is the side of equilateral triangle which we have calculated above as $2\sqrt{2}cm$ so substituting the base as $2\sqrt{2}cm$ and altitude as $\sqrt{6}cm$ in the above equation we get,
$\begin{align}
  & \dfrac{1}{2}\left( 2\sqrt{2} \right)\left( \sqrt{6} \right) \\
 & =\dfrac{1}{2}\left( 2\sqrt{2} \right)\left( \sqrt{2}\left( \sqrt{3} \right) \right) \\
 & =\dfrac{1}{2}\left( 2 \right)\left( 2 \right)\left( \sqrt{3} \right) \\
 & =2\sqrt{3}c{{m}^{2}} \\
\end{align}$
Hence, the area of equilateral triangle is equal to $2\sqrt{3}c{{m}^{2}}$

So, the correct answer is “Option A”.

Note: This question demands the knowledge of altitude and properties of equilateral triangle and trigonometric ratios. Generally, we don’t forget the properties of equilateral triangle and trigonometric ratios because it is used often in questions but the properties of altitude are not that often used so here is a tendency to forget its properties. For e.g. you might don’t know that altitude makes ${{90}^{\circ }}$ on the base of the equilateral triangle and also bisect the base of the triangle. If you don’t know this property then you could not find the side of the equilateral triangle. Hence, make sure you have understood and know these properties pretty well.