Question

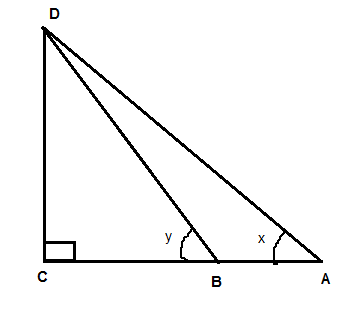
If $\tan {x^o} = \dfrac{5}{{12}},\tan {y^o} = \dfrac{3}{4}$ and AB =48m; find the length of CD.

A.50
B.45
C.40
D.55

Answer 1

Hint: In a right angled triangle, sine θ , cosine θ , tangent θ , cosecant θ , secant θ and cotangent θ can be calculated. Where θ is the angle on which the functions are getting conducted.
$\tan \theta = \dfrac{{perpendicular}}{{Base}} = \dfrac{P}{B}$
In a right angled triangle, the perpendicular is always opposite to the given angle and tangent θ is the ratio of perpendicular to the base.

Complete step-by-step answer:
In right angled triangle ACD,

$\tan x = \dfrac{P}{B} = \dfrac{{CD}}{{AC}} = \dfrac{5}{{12}}$
I.e CD = 5x
& AC = 12x
In the right angled triangle BCD ,
$\tan y = \dfrac{P}{B} = \dfrac{{CD}}{{BC}} = \dfrac{3}{4}$i.e. CD = 3y & BC =4y
Now, it is also given that AB = 48 m
Also AC= AB+ BC
$\Rightarrow$ $12x = 48 + 4y$
$\Rightarrow$ $12x - 4y = 48$
$3x - y = 12$
Also CD = CD
$5x = 3y$
 $5x - 3y = 0$
Using both the equations;
$5x - 3(3x - 12) = 0$
$\Rightarrow$ $5x - 9x + 36 = 0$
$\Rightarrow$ $ - 4x + 36 = 0$
$\Rightarrow$ $4x = 36$
$\Rightarrow$ $x = 9$
Hence, CD =5x = 5× 9 = 45m
Value of $5x = 3y$ Hence, CD=45m option(B) is correct.
Note: In a right angled triangle, the side opposite to the right angle is hypotenuse. The side opposite to the given angle is called as perpendicular and the remaining side is called as base.
$\sin \theta = \dfrac{P}{H}$
$\cos \theta = \dfrac{B}{H}$
$\tan \theta = \dfrac{P}{B}$
The tangent θ is equal to the ratio of sine θ to the cosine θ i.e. $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$. Other things we get to know about trigonometric functions are that cosecant θ is reciprocal of cosine θ and tangent is reciprocal of tangent θ .
Now, the values of sides are written proportional to each other. So, any variable was must to be added. Now, in both the triangles, CD was acting as perpendicular.