Question

If ‘T’ be any point on a tangent at any point ‘P’ of a parabola, and if TL is perpendicular to focal radius SP and TN is perpendicular to directrix, prove that \[SL=TN\]

Answer 1

Hint: We solve this problem first by drawing the figure of given data as follows

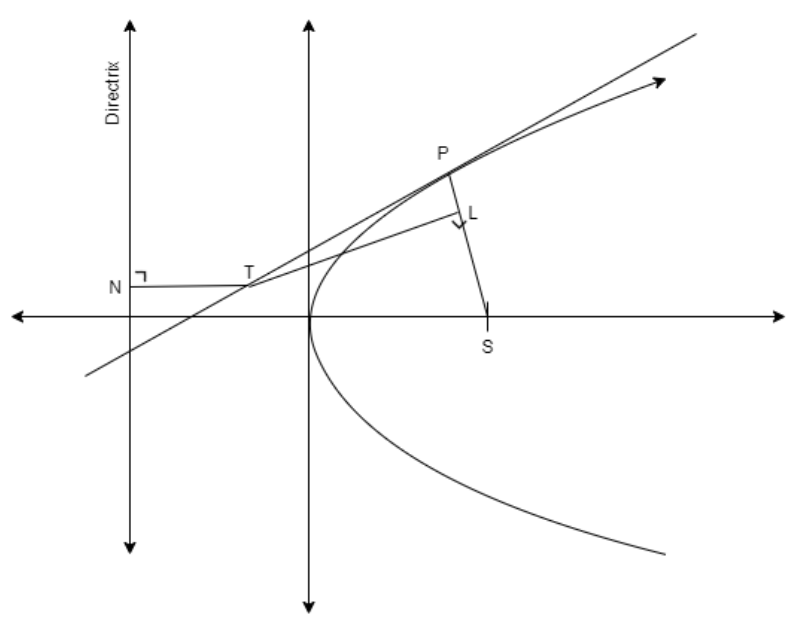
Here, we assume the parabola equation as \[{{y}^{2}}=4ax\] and the point ‘T’ as \[\left( h,k \right)\] also we use the parametric point form of P as \[\left( 2at,a{{t}^{2}} \right)\] then we find the equations of lines ‘TL’ and directrix to find the perpendicular distances SL and TN to show that both are equal.

Complete step-by-step solution:
Let us assume that the equation of parabola as
\[\Rightarrow {{y}^{2}}=4ax\]
We know that the parametric point of a parabola is given as \[\left( 2at,a{{t}^{2}} \right)\]
Let us assume that the point P as
\[\Rightarrow P=\left( 2at,a{{t}^{2}} \right)\]
We know that the focus point of parabola is \[S\left( a,0 \right)\]
Now, let us find the slope of line SP
We know that the slope of two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
By using the above formula we get the slope of SP as
\[\begin{align}
  & \Rightarrow {{m}_{1}}=\dfrac{2at-0}{a{{t}^{2}}-a} \\
 & \Rightarrow {{m}_{1}}=\dfrac{2t}{{{t}^{2}}-1} \\
\end{align}\]
Now, let us find the slope of line TL
We are given that \[TL\bot SP\]
We know that when two lines are perpendicular then the product of slopes equal to -1
So, is the slope of TL is \[{{m}_{2}}\] then we can write
\[\begin{align}
  & \Rightarrow {{m}_{1}}\times {{m}_{2}}=-1 \\
 & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\
\end{align}\]
By substituting the slope of SP we get
\[\begin{align}
  & \Rightarrow {{m}_{2}}=-\left( \dfrac{{{t}^{2}}-1}{2t} \right) \\
 & \Rightarrow {{m}_{2}}=\dfrac{1-{{t}^{2}}}{2t} \\
\end{align}\]
Now, let us assume that the point T as \[\left( h,k \right)\]
Here, we have the slope of line TL and one point T then by using the slope point form the equation of line TL can be written as
\[\Rightarrow y-k={{m}_{2}}\left( x-h \right)\]
By substituting the slope in the above equation we get
\[\Rightarrow y-k=\dfrac{1-{{t}^{2}}}{2t}\left( x-h \right)\]
By cross multiplying the above equation we get
\[\begin{align}
  & \Rightarrow 2ty-2tk=x\left( 1-{{t}^{2}} \right)-h\left( 1-{{t}^{2}} \right) \\
 & \Rightarrow x\left( 1-{{t}^{2}} \right)-2yt+2tk-h\left( 1-{{t}^{2}} \right)=0........equation(i) \\
\end{align}\]
Now, let us find the length of SL
We know that the perpendicular distance from point \[\left( {{x}_{1}},{{y}_{1}} \right)\] to the line \[ax+by+c=0\] is given as
\[\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Here, we know that the length SL is perpendicular distance from focus \[S\left( a,0 \right)\] to line TL
By using the above perpendicular distance formula we get
\[\Rightarrow SL=\dfrac{\left| a\left( 1-{{t}^{2}} \right)+2tk-h\left( 1-{{t}^{2}} \right) \right|}{\sqrt{{{\left( 1-{{t}^{2}} \right)}^{2}}+{{\left( 2t \right)}^{2}}}}\]
We know that the equation of tangent at a parametric point \[P\left( a{{t}^{2}},2at \right)\] is given as
\[\Rightarrow ty=x+a{{t}^{2}}\]
We are given that this equation of tangent passes through point \[T\left( h,k \right)\] then we get
\[\Rightarrow tk=h+a{{t}^{2}}\]
Now, by substituting the above result in the distance of SL we get
\[\begin{align}
  & \Rightarrow SL=\dfrac{\left| a-a{{t}^{2}}+2h+2a{{t}^{2}}-h+h{{t}^{2}} \right|}{\sqrt{{{\left( 1+{{t}^{2}} \right)}^{2}}}} \\
 & \Rightarrow SL=\dfrac{\left( a+h \right)\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)} \\
 & \Rightarrow SL=a+h......equation(ii) \\
\end{align}\]
Now, let us find the length of TN
We know that the equation of directrix of parabola \[{{y}^{2}}=4ax\] is given as
\[\Rightarrow x+a=0\]
Here, we can see that the length TN is the perpendicular distance from point \[T\left( h,k \right)\] to directrix because we are given that TN is perpendicular to directrix.
Now, by using the perpendicular distance formula we get
\[\begin{align}
  & \Rightarrow TN=\dfrac{\left| h+a \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
 & \Rightarrow TN=h+a.......equation(iii) \\
\end{align}\]
Now, from the equation (ii) and equation (iii) we get
\[\Rightarrow SL=TN\]
Therefore, the required result has been proved.

Note: Here we used the general type of parabola but we can use any type of parabola to get the required result. For the parabola \[{{y}^{2}}=4ax\] we used some standard formulas such as
(i) Parametric point is given as \[\left( 2at,a{{t}^{2}} \right)\]
(ii) Equation of tangent at any point \[\left( 2at,a{{t}^{2}} \right)\] is given as
\[\Rightarrow ty=x+a{{t}^{2}}\]
(iii) Directrix is given as
\[\Rightarrow x+a=0\]
(iv) The perpendicular distance from point \[\left( {{x}_{1}},{{y}_{1}} \right)\] to the line \[ax+by+c=0\] is given as
\[\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
These are important results to be remembered while solving this problem.