Question

If $ \sin \theta =\dfrac{3}{5} $ , find the values of other trigonometric ratios.

Answer 1

Hint: Consider a right angled $ \Delta ABC $ , right angled at B. Use Pythagoras theorem then find the values of $ \cos \theta , \tan \theta $ and their inverse $ \csc \theta,\sec \theta $ and $ \cot \theta $

Complete step-by-step answer:
Let us consider a right angled triangle ABC. We know the Pythagoras theorem, also known as Pythagoras theorem; it is a fundamental relation in Euclidean geometry among the 3 sides of a right triangle.

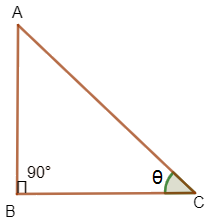
It states that the area of the squares whose sides is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
 $ A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} $
We have been given, $ \sin \theta =\dfrac{3}{5} $ .
In the triangle ABC, $ \angle B=90{}^\circ $
And take $ \angle C=\theta $
Here, $ \sin \theta = $ opposite side/hypotenuse = $ \dfrac{AB}{BC} $
 $ \cos \theta = $ Adjacent side/hypotenuse = $ \dfrac{BC}{AC} $
Given, $ \sin \theta =\dfrac{3}{5} $
AB=3 and AC=5
Using the Pythagoras theorem, $ A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} $
 $ \begin{align}
& {{5}^{2}}={{3}^{2}}+B{{C}^{2}} \\
& \Rightarrow B{{C}^{2}}={{5}^{2}}-{{3}^{2}} \\
& \Rightarrow BC=\sqrt{25-9}=\sqrt{16}=4 \\
& \therefore \cos \theta =\dfrac{4}{5} \\
\end{align} $
 $ \tan \theta = $ Opposite side/adjacent side= $ \dfrac{AB}{BC}=\dfrac{3}{4} $
 $ \csc\theta =\dfrac{1}{\sin \theta }=\dfrac{1}{\dfrac{3}{5}}=\dfrac{5}{3} $
 $ \begin{align}
& \sec \theta =\dfrac{1}{\cos \theta }=\dfrac{1}{\dfrac{4}{5}}=\dfrac{5}{4} \\
& \cot \theta =\dfrac{1}{\tan \theta }=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3} \\
& \therefore \sin \theta =\dfrac{3}{5},\cos \theta =\dfrac{4}{5},\tan \theta =\dfrac{3}{4} \\
& \csc\theta =\dfrac{5}{3},\sec \theta =\dfrac{5}{4},\cot \theta =\dfrac{4}{3} \\
\end{align} $

Note: There are three types of special right triangle, 30-60-90 triangle, 45-45-90 triangle and Pythagoras triple triangles. This problem was based on trigonometric ratios. So we just need to remember all the formulas of trigonometric ratio in the form of perpendicular, base and hypotenuse.