Question

If $\sin \alpha = \dfrac{{ - 3}}{5}$, where $\pi < \alpha < \dfrac{{3\pi }}{2}$ then, $\dfrac{{\cos \alpha }}{2} = $
A. $\dfrac{{ - 1}}{{\sqrt {10} }}$
B. $\dfrac{1}{{\sqrt {10} }}$
C. $\dfrac{3}{{\sqrt {10} }}$
D. $\dfrac{{ - 3}}{{\sqrt {10} }} $

Answer 1

Hint:The given problem has only the $\sin $ function and we are supposed to find the $\cos $ function. A range is also given, so we can first find out in which quadrant the function lies. For the given value of angle, we can find $\cos $ value. Then we move on to finding out the final answer.

Formula used:
$\cos 2A = 2{\cos ^2}A - 1$

Complete step by step answer:
The given expression is as follows,
$\sin \alpha = \dfrac{{ - 3}}{5}$
We know that,
$\sin \alpha = \dfrac{\text{opposite}}{\text{hypotenuse}}$
We will consider the following right-angle triangle

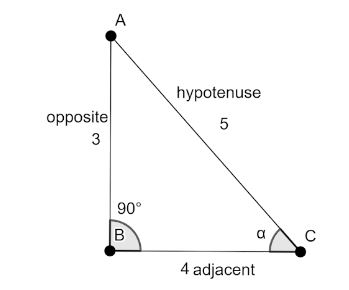
The range for the angle $\alpha $is given as
$\pi < \alpha < \dfrac{{3\pi }}{2}$
From the above, we can figure out that $\alpha $ lies in the Quadrant III. In Quadrant III both $\sin $ and the $\cos $functions are negative.
We now, will find out the range of $\dfrac{{\cos \alpha }}{2}$
The range is $\pi < \alpha < \dfrac{{3\pi }}{2}$
To find out the range of $\dfrac{\alpha }{2}$ divide the given range by two completely.
$\dfrac{\pi }{2} < \dfrac{\alpha }{2} < \dfrac{{3\pi }}{4}$
This is the range of Quadrant II. The $\cos $ function is negative in the Quadrant II as well.
If, $\sin \alpha = \dfrac{{ - 3}}{5}$
Then, using Pythagoras theorem, we have
$\cos \alpha = \dfrac{{ - 4}}{5}$

Using the above-mentioned formulas,
$\cos \alpha = 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right) - 1$
We know the value of $\cos \alpha $
By substituting, we get
$ \Rightarrow \dfrac{{ - 4}}{5} = 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right)$
Rearranging the equation to get $\cos \left( {\dfrac{\alpha }{2}} \right)$ on the LHS,
$\Rightarrow 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right) = 1 - \dfrac{4}{5}
\Rightarrow {\cos ^2}\left( {\dfrac{\alpha }{2}} \right) = \dfrac{1}{10} $
Removing the square on both the sides, we get
$\cos \left( {\dfrac{\alpha }{2}} \right) = \sqrt {\dfrac{1}{{10}}} $
Since $\dfrac{\alpha }{2}$ lies in Quadrant II, the $\cos $ function will be negative.
Therefore, the final answer is $\cos \left( {\dfrac{\alpha }{2}} \right) = \dfrac{{ - 1}}{{\sqrt {10} }}$

Hence, option A is the correct answer.

Note:Noting down the quadrant and whether the function will be positive or negative is an important aspect. If the wrong sign is put, the final answer will be wrong. In the last step do not keep the root for the whole number because negative roots cannot be defined.