Question

If \[\sin A = \dfrac{3}{4},\,\] find all other Trigonometric-ratios.

Answer 1

Hint: In this we have one Trigonometric-ratio equal to value that does not belong to the standard angle table.
∴ We apply triangle concept in it.

Formula used: \[\cos A = \dfrac{{base}}{{hyp}},\,\tan A = \dfrac{{perp}}{{base}},\operatorname {cotA} = \dfrac{{base}}{{perp}}, \sec A = \dfrac{{hyp}}{{base}}, cosecA = \dfrac{{hyp}}{{perp}}\]
By Pythagoras theorem: \[{(hyp)^2} = {(perp)^2} + {(base)^2}\]

Complete step by step answer:
(1) Given: Trigonometric-ratio, \[sinA = \dfrac{3}{4}\,\]
 Also, we know that \[sinA = \dfrac{{perp}}{{hyp}}\]
∴ On comparing, we have
Perpendicular $ = 3$ and hypotenuse $ = 4$
(2) Draw a right angle ΔABC, right angle at B \[(A \ne 90^\circ )\]

(3) Mention two sides \[AC = 4,{\text{ }}BC = 3\]

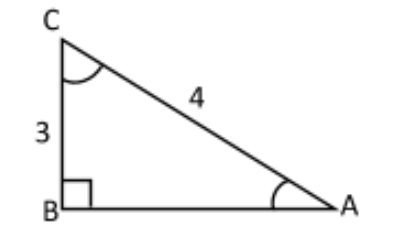
(4) To get the third side in the right angle triangle, we apply Pythagoras theorem.
(5) Using Pythagoras, we calculate base
\[{\left( {hyp} \right)^2} = {(perp)^2} + {(base)^2}\]
\[ \Rightarrow {(4)^2} = {(3)^2} + {(base)^2}\]
$ \Rightarrow 16 = 9 + {(base)^2}$
\[ \Rightarrow 16 - 9 = {(base)^2}\]
\[ \Rightarrow {(base)^2} = 7\]
\[ \Rightarrow base = \sqrt 7 \]
(6) As from above, we got all three sides of the right angle triangle ABC.

(7) Using formula to find various Trigonometric-ratios,
\[
  \cos A = \dfrac{{base}}{{hyp.}} \Rightarrow \dfrac{{\sqrt 7 }}{4}\,\,\, \\
  \tan A = \dfrac{{perp}}{{base}} = \dfrac{3}{{\sqrt 7 }} \\
  \cot A = \dfrac{{base}}{{perp}} = \dfrac{{\sqrt 7 }}{3} \\
  \sec A = \dfrac{{hyp}}{{base}} = \dfrac{4}{{\sqrt 7 }}\,\, \\
  \operatorname{cosec} A = \dfrac{{hyp}}{{perp}} = \dfrac{4}{3} \\
 \]

Note: In trigonometry, there are six functions of an angle commonly used. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (cosec). These six trigonometric functions are in relation to a right triangle displayed in the figure.
Use trigonometric ratios. Here, cosecA is a reciprocal of sinA and in the same way secA is a reciprocal of cosA, cotA is a reciprocal of tanA.