Question

If similar triangles, $\Delta ABC\sim \Delta DEF$ in which $AH$ and $DY$ are the bisectors of $\angle A$ and $\angle D$ respectively. If $AH=6.5\,\text{ cm}$ and $DY=5.2\text{ cm}$ , find the ratio of the area of $\Delta ABC$ and $\Delta DEF$ .

Answer 1

Hint: In this problem we need to calculate the ratio of the area of $\Delta ABC$ and $\Delta DEF$ where $\Delta ABC\sim \Delta DEF$. We know that the ratio of the areas of two similar triangles is equal to the square of ratios of corresponding sides or corresponding altitudes or corresponding medians or corresponding angle bisectors. In the problem they have mentioned that $AH$ and $DY$ are the bisectors of $\angle A$ and $\angle D$ respectively. So we will calculate the ratio of the corresponding bisectors after that we will calculate the square of the obtained ratio which is our required value.

Complete step by step answer:
Given that, $\Delta ABC\sim \Delta DEF$.
Let the triangles be

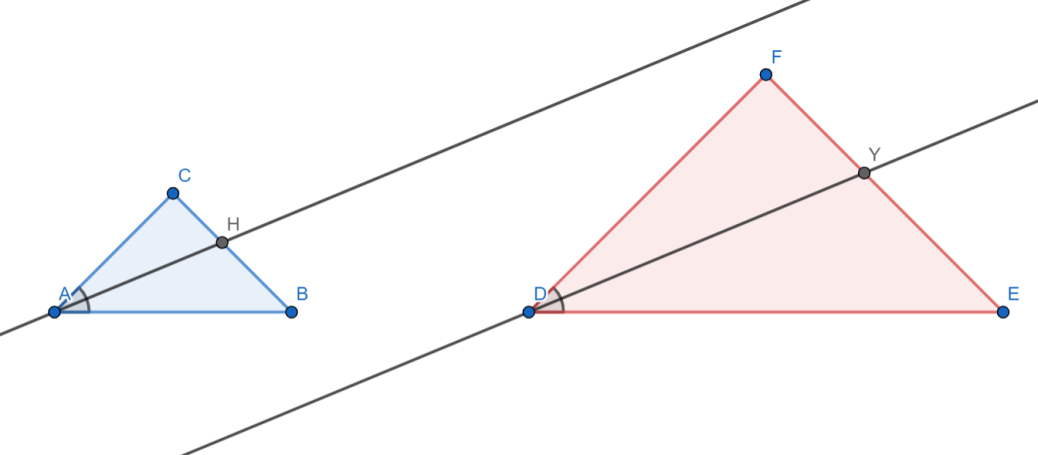
In the problem they have mentioned that $AH$ and $DY$ are the bisectors of $\angle A$ and $\angle D$ respectively as shown in above figure.
The length of segment $AH$ is $AH=6.5\,\text{ cm}$.
The length of the segment $DY$is $DY=5.2\text{ cm}$.
The ratio of the corresponding angle bisectors is given by
$\dfrac{AH}{DY}=\dfrac{6.5}{5.2}$
Multiplying and dividing the right sides of the above equation with $10$ , then we will get
$\begin{align}
  & \dfrac{AH}{DY}=\dfrac{6.5}{5.2}\times \dfrac{10}{10} \\
 & \Rightarrow \dfrac{AH}{DY}=\dfrac{65}{52} \\
\end{align}$
Writing the terms in the above equation in their factorization form, then we will have
$\begin{align}
  & \dfrac{AH}{DY}=\dfrac{5\times 13}{4\times 13} \\
 & \Rightarrow \dfrac{AH}{DY}=\dfrac{5}{4} \\
\end{align}$
We know that the ratio of areas of the two similar triangles is equal to the square of ratios of corresponding angle bisectors. So the ratio of areas of $\Delta ABC$ and $\Delta DEF$ is given by
$\begin{align}
  & \dfrac{{{A}_{1}}}{{{A}_{2}}}={{\left( \dfrac{AH}{DY} \right)}^{2}} \\
 & \Rightarrow \dfrac{{{A}_{1}}}{{{A}_{2}}}={{\left( \dfrac{5}{4} \right)}^{2}} \\
 & \Rightarrow \dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{25}{16} \\
\end{align}$
Hence the ratio of areas of $\Delta ABC$ and $\Delta DEF$ is $25:16$ .
Note: In this problem we have given the angle bisectors of $\angle A$ and $\angle D$ which are corresponding angles in the similar triangles. So we have considered the angle bisectors as corresponding angle bisectors. If they have given bisectors of any other angles, then we need to check them whether the angles are corresponding to each other or not by drawing the triangles after which we can proceed for the calculation.