Question

If sec C is \[\dfrac{m}{2\sqrt{2}}\], then value of m is:

(a) 1
(b) 3
(c) 7
(d) 5

Answer 1

Hint: We will apply Pythagoras rule to find the unknown sides in both right angle triangles ABD and BCD. Then we will use the definition of cos that is base by hypotenuse to find cos C and then the reciprocal of this value will be sec C. Finally, we will compare this calculated value of sec C with the given value and then we will get the answer.

Complete step-by-step answer:
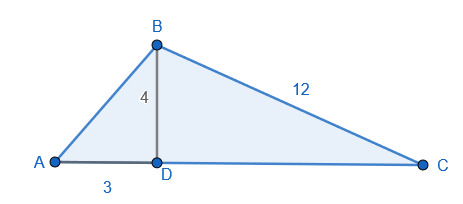
It is mentioned in the question from the figure that a perpendicular from B on AC cuts AC at point D such that \[\angle BDA=\angle BDC={{90}^{\circ }}\].
Also from the figure we can see that AD is equal to 3, BD is equal to 4 and BC is equal to 12.
Now applying pythagoras rule in triangle ABD where base is AD, perpendicular is BD and hypotenuse is AB and hence we get,
\[A{{B}^{2}}=B{{D}^{2}}+A{{D}^{2}}.......(1)\]
Substituting the values of BD and AD in equation (1) we get,
\[A{{B}^{2}}={{3}^{2}}+{{4}^{2}}.......(2)\]
Now squaring both the terms in the right hand side first and then adding them in equation (2) we get,
\[A{{B}^{2}}=9+16=25........(3)\]
Now taking the square root of both the sides in equation (3) we get the hypotenuse AB,
\[AB=\sqrt{25}=5........(4)\]
Now again applying the pythagoras rule in triangle BCD where base is CD, perpendicular is BD and hypotenuse is BC and hence we get,
\[B{{C}^{2}}=B{{D}^{2}}+C{{D}^{2}}.......(5)\]
Substituting the values of BD and BC in equation (5) we get,
\[{{12}^{2}}={{4}^{2}}+C{{D}^{2}}.......(6)\]
Now squaring both the constant terms and then subtracting them in equation (6) and rearranging we get,
\[C{{D}^{2}}=144-16=128.......(7)\]
Now taking the square root of both the sides in equation (7) we get the hypotenuse CD,
\[CD=\sqrt{128}=8\sqrt{2}.......(8)\]
Now we know that sec C is reciprocal of cos C and cos C is base CD divided by hypotenuse BC in triangle BCD. So sec C is hypotenuse BC divided by base CD.
\[\sec C=\dfrac{hypotenuse}{base}=\dfrac{BC}{CD}.......(9)\]
Now substituting the value of CD from equation (8) in equation (9) and BC is known to us. So we get,
\[\sec C=\dfrac{12}{8\sqrt{2}}=\dfrac{3}{2\sqrt{2}}.......(10)\]
Now comparing the value in equation (10) with \[\dfrac{m}{2\sqrt{2}}\], we get m equal to 3. Hence the correct answer is option (b).

Note: Remembering the Pythagoras formula and basic definition of cos is the key here. We can make a mistake in substituting the value of hypotenuse in place of perpendicular and hence we need to be careful while doing this step.