Question

If ${S_1}$ and ${S_2}$ are two coherent sources of the sound of frequency \[110Hz\] each. They have no initial phase difference. The intensity at a point P due to ${S_1}$ is \[{I_0}\] and due to ${S_2}$ is \[4{I_0}\] . If the velocity of sound is \[330m/s\] then the resultant intensity at P is

a. \[{I_0}\]
b. \[9{I_0}\]
c. \[3{I_0}\]
d. \[8{I_0}\]

Answer 1

Hint: The frequency and velocity of the sound wave are given. Find the wavelength of the wave.
Use the information given in the diagram and find the path difference.
calculate the path difference by the path difference.
Use the intensity formula for two waves after interference and put the phase difference in this formula to get the resultant intensity.

Formula used:
The wavelength, $\lambda = \dfrac{{V{\text{(velocity of sound wave)}}}}{{f{\text{(frequency)}}}}$
The path difference, $x = {S_2}P - {S_1}P$
The phase difference, $\phi = \dfrac{{2\pi x}}{\lambda }$
The resultant intensity after the interference of two waves, $I = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} \cos \phi $
${I_1},{I_2}$ are the intensities of the two waves.

Complete step by step answer:
${S_1}$ and ${S_2}$ are the two coherent sources of the sound waves. The frequency of each wave is $f = 110Hz$
After the interference of two waves of the intensities ${I_1},{I_2}$ [${I_1} = {I_0}$ and ${I_2} = 4{I_0}$
], the resultant intensity will be,
$I = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} \cos \phi $ , $\phi $ is the phase difference.
The phase difference can be described by, $\phi = \dfrac{{2\pi x}}{\lambda }$
Where, $\lambda $ is The wavelength and $x$ is The path difference.
$\lambda = \dfrac{{V{\text{(velocity of sound wave)}}}}{{f{\text{(frequency)}}}} = \dfrac{{330}}{{110}}$
$\therefore \lambda = 3m$
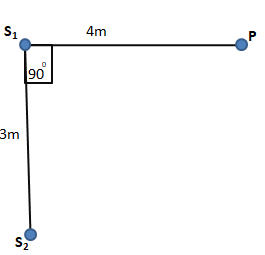
The path difference, $x = {S_2}P - {S_1}P$

From the figure, ${S_2}P = \sqrt {{4^2} + {3^2}} = 5$ [ since this is a right-angle triangle]
$\therefore x = {S_2}P - {S_1}P = 5 - 4 = 1m$
$\therefore \phi = \dfrac{{2\pi x}}{\lambda } = 2\pi \dfrac{1}{3} = \dfrac{{2\pi }}{3}$
Now, $I = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} \cos \phi $
${I_1} = {I_0}$ and ${I_2} = 4{I_0}$
$\cos \phi = \cos \dfrac{{2\pi }}{3} = - \dfrac{1}{2}$
$\therefore I = {I_0} + 4{I_0} + 2\sqrt {{I_0} \times 4{I_0}} \left( { - \dfrac{1}{2}} \right)$
$ \Rightarrow I = 5{I_0} - \sqrt {{I_0} \times 4{I_0}} $
$ \Rightarrow I = 5{I_0} - 2{I_0}$
$ \Rightarrow I = 3{I_0}$
So the resultant intensity of the two waves after the interference, $ \Rightarrow I = 3{I_0}$

Hence, the correct answer is option (C).

Additional information:
• The coherent sources are most important for interference.
• When the two waves of the same wavelengths and same frequency superpose, interference occurs.
• The phase difference of the two waves for which the interference occurs should be constant.

Note: The relation between the intensity and the amplitude will be, $I \propto {A^2}$.
Let, the amplitudes of the two waves are ${A_1}$ and ${A_2}$, and the phase difference is $\phi $.
If the two waves are superposed, the resultant amplitude $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \phi }$.