Question

If \[S\] is the set of all real \[x\] and such that \[\dfrac{2x-1}{2{{x}^{3}}+3{{x}^{2}}+x}\] is positive, then \[S\] contains
(a).\[\left( -\infty ,-\dfrac{3}{2} \right)\]
(b).\[\left( -\dfrac{3}{2},-\dfrac{1}{4} \right)\]
(c).\[\left( -\dfrac{1}{4},\dfrac{1}{2} \right)\]
(d).\[\left( \dfrac{1}{2},3 \right)\]

Answer 1

Hint: In the given question, we have been asked the sets of solutions that satisfy the equation. In order to answer the question, we will simplify the equation given and then find the values of ‘x’ that will satisfy the equation given in the question and then check the each interval for which the condition that is given in the question will satisfy.

Complete step by step solution:
We have given the equation,
\[\Rightarrow \dfrac{2x-1}{2{{x}^{3}}+3{{x}^{2}}+x}\]
It is given that, \[S\]is the set of all real \[x\]
Thus,
\[\Rightarrow \dfrac{2x-1}{2{{x}^{3}}+3{{x}^{2}}+x}>0\]
Taking \[x\] as a common factor from denominator, we get
\[\Rightarrow \dfrac{2x-1}{x\left( 2{{x}^{2}}+3x+1 \right)}>0\]
Simplifying the quadratic equation in the denominator by splitting the middle term, we get
\[\Rightarrow \dfrac{2x-1}{x\left( 2{{x}^{2}}+2x+1x+1 \right)}>0\]
\[\Rightarrow \dfrac{2x-1}{x\left( 2x\left( x+1 \right)+1\left( x+1 \right) \right)}>0\]
Taking out the common factor in denominator, we get
\[\Rightarrow \dfrac{2x-1}{x\left( 2x+1 \right)\left( x+1 \right)}>0\]
Solving the factors individually by equate them equal to 0 for the values of \[x\],
\[\Rightarrow 2x-1=0\] and \[x=0\]and \[2x+1=0\] and \[x+1=0\]
Solving each for the values of \[x\], we get
\[\Rightarrow x=\dfrac{1}{2}\ and\ x=0\ and\ x=-\dfrac{1}{2}\ and\ x=-1\]
Therefore,
The values of \[x\] are \[\dfrac{1}{2},0,-\dfrac{1}{2}\ and\ -1\].
Represents the values of \[x\] on the number line.

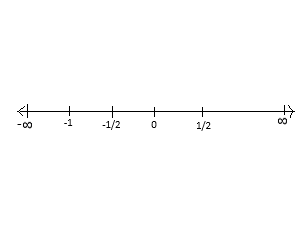
Check the solution for each interval,
If \[x\in \left( -\infty ,-1 \right)\], take any value between this interval, you will get a positive solution.
If \[x\in \left( -1,-\dfrac{1}{2} \right)\], take any value between this interval, you will get a negative solution.
If \[x\in \left( -\dfrac{1}{2},0 \right)\], take any value between this interval, you will get a positive solution.
If \[x\in \left( 0,\dfrac{1}{2} \right)\], take any value between this interval, you will get a negative solution.
If \[x\in \left( \dfrac{1}{2},\infty \right)\], take any value between this interval, you will get a positive solution.
Here, we carefully examine that \[x\] will not be equal to \[0,-\dfrac{1}{2},\ and\ -1\] because this will make the denominator 0, which will make the equation given is equal to not defined.
Therefore,
\[\Rightarrow x\in \left( -\infty ,-\dfrac{1}{2} \right)\cup \left( -\dfrac{1}{2},0 \right)\cup \left( \dfrac{1}{2},\infty \right)\]
From the option given in the question, only the option (a) and option (d) satisfy the above equation.

Therefore, option (a) and the option (d) are the correct solution.

Note:
In order to solve these types of questions, you should remember the basic method to solving the quadratic equation. We have to form the condition of the set of ranges for x, then by combining all the conditions we will get the set of real values of x that will satisfy the equation and the condition given in the question.