Question

If \[{\rm P}\] and \[Q\] are two distinct points on the parabola, \[{y^2} = 4x\] , with parameters \[t\] and \[{t_1}\] respectively. If the normal at \[{\rm P}\] passes through \[Q\] , then the minimum value \[t_1^2\] is:
A. \[8\]
B. \[4\]
C. \[6\]
D. \[2\]

Answer 1

Hint: In order to determine the minimum value of \[t_1^2\] . First, we compare the given parabola equation \[{y^2} = 4x\] with the parameter \[t\] and \[{t_1}\] . The equation of the normal parametric form \[{\rm P}\] to the parabola \[{y^2} = - 4ax\] at the point \[{\rm P}(a{t^2},2at)\] and \[Q(t_1^2,2a{t_1})\] of the parametric equation is \[t - yx = 2at + a{t^3}\] and put the value of \[a = 1\] into the intersection point then simplify it and get the normal parameter value.

Complete step-by-step answer:
We are given an equation on the parabola \[{y^2} = 4(1)x\] and the intersection point \[{\rm P}(a{t^2},2at)\] and \[Q(t_1^2,2a{t_1})\] of the equation \[t - yx = 2at + a{t^3}\]
In this equation we are supposed to find out the equation of line which is passing through the point \[{\rm P}({t^2},2t)\] and \[Q(t_1^2,2{t_1})\] of a normal parametric equation \[y + tx = 2t + {t^3}\] . Where, the value \[a = 1\] and the parameters \[t\] and \[{t_1}\] .
The normal equation \[tx - y = 2t + {t^3}\] is compared with \[y + tx = 2at + a{t^3}\] which is intersect with two distinct point \[{\rm P}({t^2},2t)\] and \[Q(t_1^2,2{t_1})\] .
The normal parametric form at the point \[{\rm P}({t^2},2t)\] of the equation is \[tx - y = 2t + {t^3}\] passes through the point \[Q(t_1^2,2{t_1})\] .
So the equation is \[tt_1^2 - 2{t_1} = 2t + {t^3}\] .
By simplify it in further step, we get
 \[tt_1^2 - {t^3} = 2t + 2{t_1}\]
Now we get
 \[t(t_1^2 - {t^2}) = 2(t + {t_1})\]
When comparing the formula \[({a^2} - {b^2}) = (a - b)(a + b)\] with the equation and expand it as \[t({t_1} - t)({t_1} + t) = 2(t + {t_1})\] , so, By dividing the common on both side by \[(t + {t_1})\]
 \[t({t_1} - t) = 2\]
Expanding the factors on RHS, we get
 \[{t_1} = \dfrac{2}{t} + t \geqslant 2\sqrt 2 \] . since \[\left[ {\dfrac{{\dfrac{2}{t} + t}}{2} \geqslant 2\sqrt 2 } \right] \]
We require the minimum value \[t_1^2\] is \[{(2\sqrt 2 )^2} = 8\]
Therefore, the minimum values of \[t_1^2\] is \[8\] through the equation \[tt_1^2 - {t^3} = 2t + 2{t_1}\] and passes the point is \[{\rm P}({t^2},2t)\] and \[Q(t_1^2,2{t_1})\] .
As a result, the option A: \[8\] is the right answer
So, the correct answer is “Option A”.

Note: The graph of the parabola and the normal parametric line is plotted below.
The curve of the parabola is \[y = 4x\] and the line that passes through the parabola is \[t - yx = 2at + a{t^3}\] .

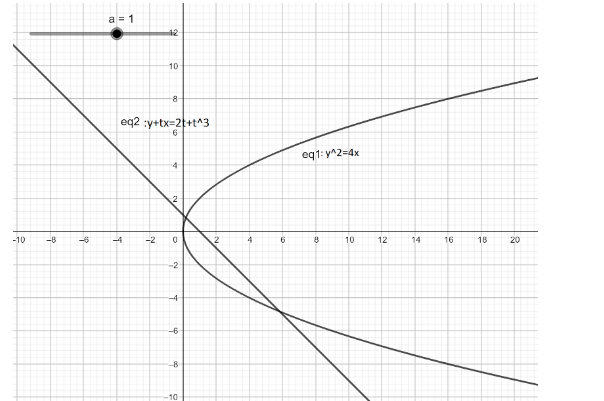
To find the distinct point \[{\rm P}(a{t^2},2at)\] and \[Q(t_1^2,2a{t_1})\] from the equation \[t - yx = 2at + a{t^3}\] . Where the value, \[a = 1\] .
Finally we got the minimum value of \[t_1^2\] from the equation of normal parameters \[t\] and \[{t_1}\] .