
If $P,Q,R$ and $S$ are represented by the complex numbers $4+i,1+6i,-4+3i$ and $-1-2i$ respectively, then $PQRS$ is a
\[\begin{array}{*{35}{l}}
\left( A \right)Rectangle \\
\left( B \right)Square \\
\begin{align}
& \left( C \right)Rhombus \\
& \left( D \right)Parallelogram \\
\end{align} \\
\end{array}\]
Answer
553.8k+ views
Hint: We first convert the complex numbers into points with $\left( x,y \right)$ coordinates. Then, we find the distance between the adjacent points and check if they are equal or not. Then, we check for the angle between any two adjacent sides and check if it is ${{90}^{\circ }}$ . After these two conditions, we can declare the four sided polygon to be a square, rhombus, rectangle or parallelogram.
Complete step by step answer:
Any complex number \[z\] is represented by the form $x+iy$ where $x$ is the real part and $y$ is the imaginary part. The complex number $z$ can be shown on an argand plane by the point with coordinates $\left( x,y \right)$ .
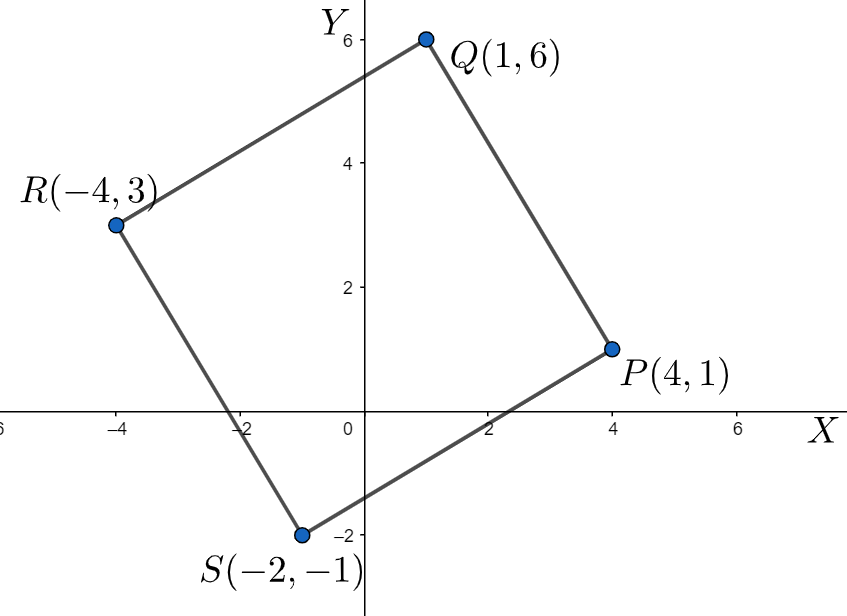
In our problem, we have four complex numbers $P,Q,R,S$ with values $4+i,1+6i,-4+3i,-1-2i$ . This means that on an argand plane, these numbers are nothing but the points with coordinates $\left( 4,1 \right),\left( 1,6 \right),\left( -4,3 \right),\left( -1,-2 \right)$ .
$PQRS$ is a polygon with four sides. We know that the distance between two points on the $x-y$ plane can be known using the formula,
$\sqrt{{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}$
Where, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are two points between which we have to find the difference. Applying this formula to find the distance between the adjacent points, we get
Distance between $P$ and $Q$ $=\sqrt{{{\left( 6-1 \right)}^{2}}+{{\left( 1-4 \right)}^{2}}}=5.83$
Distance between $Q$ and $R$ $=\sqrt{{{\left( 3-6 \right)}^{2}}+{{\left( -4-1 \right)}^{2}}}=5.83$
Distance between $R$ and $S$ $=\sqrt{{{\left( -2-3 \right)}^{2}}+{{\left( -1+4 \right)}^{2}}}=5.83$
Distance between $S$ and $P$ $=\sqrt{{{\left( 1+2 \right)}^{2}}+{{\left( 4+1 \right)}^{2}}}=5.83$
We see that all these distances are equal. This means that all the sides of the polygon $PQRS$ are of equal length. Now, there are two possibilities that can be inferred from this result: rhombus or square. If we can prove that the angle between any two adjacent sides is ${{90}^{\circ }}$ , then it is a square, else not.
For this, let us find the angle between the sides $PQ$ and $QR$ . We know that the slope of a line joining two points can be known using the formula
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
So, the slope of the line $PQ$ is
${{m}_{1}}=\dfrac{6-1}{1-4}=-\dfrac{5}{3}$
And that of line $QR$ is
${{m}_{2}}=\dfrac{3-6}{-4-1}=\dfrac{3}{5}$
We see that the two slopes are negative reciprocals of one another. This means that the two lines $PQ$ and $QR$ are perpendicular to each other.
Therefore, we can prove that $PQRS$ is a square.
Note: The negatives signs in the complex numbers must be considered carefully while plotting the points. All the formulae, including the distance formulae and the slope formula must be executed carefully, keeping in mind the negative signs and the $x$ and $y$ coordinates. This problem can also be solved by plotting the points first and then checking the length using the scale and the angles using a protractor.
Complete step by step answer:
Any complex number \[z\] is represented by the form $x+iy$ where $x$ is the real part and $y$ is the imaginary part. The complex number $z$ can be shown on an argand plane by the point with coordinates $\left( x,y \right)$ .
In our problem, we have four complex numbers $P,Q,R,S$ with values $4+i,1+6i,-4+3i,-1-2i$ . This means that on an argand plane, these numbers are nothing but the points with coordinates $\left( 4,1 \right),\left( 1,6 \right),\left( -4,3 \right),\left( -1,-2 \right)$ .
$PQRS$ is a polygon with four sides. We know that the distance between two points on the $x-y$ plane can be known using the formula,
$\sqrt{{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}$
Where, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are two points between which we have to find the difference. Applying this formula to find the distance between the adjacent points, we get
Distance between $P$ and $Q$ $=\sqrt{{{\left( 6-1 \right)}^{2}}+{{\left( 1-4 \right)}^{2}}}=5.83$
Distance between $Q$ and $R$ $=\sqrt{{{\left( 3-6 \right)}^{2}}+{{\left( -4-1 \right)}^{2}}}=5.83$
Distance between $R$ and $S$ $=\sqrt{{{\left( -2-3 \right)}^{2}}+{{\left( -1+4 \right)}^{2}}}=5.83$
Distance between $S$ and $P$ $=\sqrt{{{\left( 1+2 \right)}^{2}}+{{\left( 4+1 \right)}^{2}}}=5.83$
We see that all these distances are equal. This means that all the sides of the polygon $PQRS$ are of equal length. Now, there are two possibilities that can be inferred from this result: rhombus or square. If we can prove that the angle between any two adjacent sides is ${{90}^{\circ }}$ , then it is a square, else not.
For this, let us find the angle between the sides $PQ$ and $QR$ . We know that the slope of a line joining two points can be known using the formula
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
So, the slope of the line $PQ$ is
${{m}_{1}}=\dfrac{6-1}{1-4}=-\dfrac{5}{3}$
And that of line $QR$ is
${{m}_{2}}=\dfrac{3-6}{-4-1}=\dfrac{3}{5}$
We see that the two slopes are negative reciprocals of one another. This means that the two lines $PQ$ and $QR$ are perpendicular to each other.
Therefore, we can prove that $PQRS$ is a square.

Note: The negatives signs in the complex numbers must be considered carefully while plotting the points. All the formulae, including the distance formulae and the slope formula must be executed carefully, keeping in mind the negative signs and the $x$ and $y$ coordinates. This problem can also be solved by plotting the points first and then checking the length using the scale and the angles using a protractor.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE




