Question

If possible maximize z = x+4y, subject to $ 3x+6y\le 6,4x+8y\ge 16 $ and $ x\ge 0,y\ge 0 $

Answer 1

Hint: Plot these lines on a graph paper. Recall that the optimum value lies on the corners of the graph formed. Hence find the value of the target function at the corners of the graph and hence determine the minima of the target function.

Complete step-by-step answer:
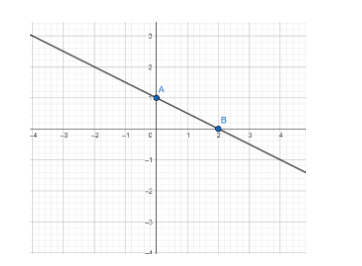
Plotting 3x+6y = 6 on the graph.
When x=0, we have
6y =6
i.e. y =1
When y=0, we have
3x=6
i.e. x =2
Hence two points on the line are (0,1) and (2,0)
Plot these two points on the graph paper and join the points.

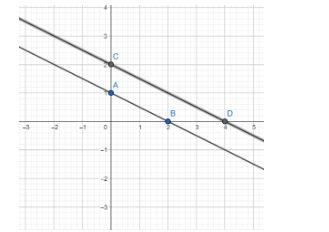
Plotting 4x+8y = 16
When x = 0, we have
8y = 16.
i.e. y = 2
When y = 0, we have
4x = 16
i.e. x = 4
Hence two points on the line are (0,2) and (4,0)
Plot these two points on the graph paper and join the points.

Also, we have $ x\ge 0,y\ge 0 $

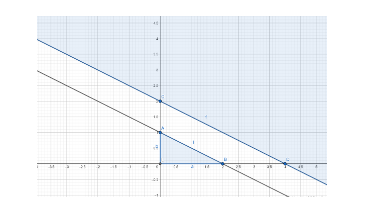
The feasible region is shown as above.
We draw the graphs of the lines x+4y = 1 and x+4y = 2 as shown below

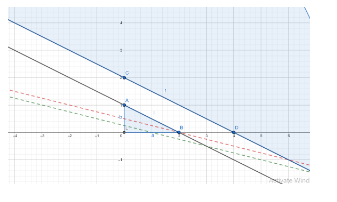
Green dashed line is x+4y = 1
Red dashed line is x+4y = 2
As can be observed from the graph as the value of c increases the graph of the line x+4y = c shifts upwards.
Since the feasible region is not bounded, the maxima of the target function z = x+4y does not exist under the given constraints.

Note: [1] Keeping the variables of the constraints non-negative is important for the solution of a linear programming problem.
[2] You can also apply the simplex method to find the minima of the above problem.
The simplex method is an algorithmic process of finding the optima of Linear programming problems.