Question

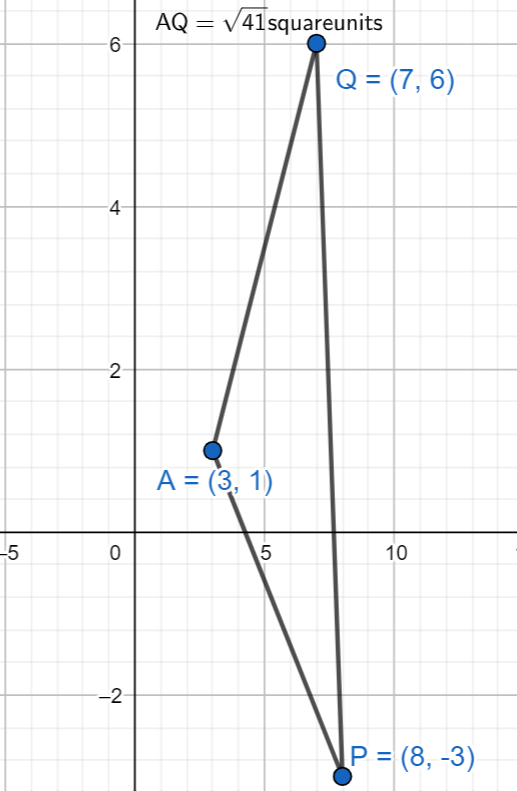
If point \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\], find the value of y and find the distance AQ.

Answer 1

Hint: In this problem, we have to find the value of y and find the distance AQ. We are given that If \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\]. We know that, since \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\],then AP will be equal to AQ. We can find the value of y by equating AP and AQ, we can then find the distance by using distance between two points formula.

Complete step-by-step solution:
We know that the given points are,
\[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\]
We also know that \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\].
Since \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\],then AP will be equal to AQ.
AQ = AP.
We also know that the distance formula is,
\[\Rightarrow \sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+\left( {{y}_{1}}-{{y}_{2}} \right)}\] …… (1)
Where in AQ,
\[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,y \right),\left( {{x}_{2}},{{y}_{2}} \right)=\left( 8,-3 \right)\]
Where in AP,
 \[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,y \right),\left( {{x}_{2}},{{y}_{2}} \right)=\left( 7,6 \right)\]
We can now substitute these values in (1) to find AP, we get
AP = \[\sqrt{{{\left( 3-8 \right)}^{2}}+{{\left( y-\left( -3 \right) \right)}^{2}}}=\sqrt{{{\left( -5 \right)}^{2}}+{{\left( y+3 \right)}^{2}}}\]
We can now simplify the above step, we get
AP = \[\sqrt{25+{{y}^{2}}+9+6y}\]………. (2)
We can now substitute these values in (1) to find AQ, we get
AQ = \[\sqrt{{{\left( 3-7 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}=\sqrt{{{\left( -4 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}\]
We can now simplify the above step, we get
AQ = \[\sqrt{16+{{y}^{2}}+36-12y}\] ……… (3)
We can now equate (2) and (3).
\[\Rightarrow \sqrt{25+{{y}^{2}}+9+6y}=\sqrt{16+{{y}^{2}}+36-12y}\]
We can now take square on both side, to remove the square root, we get
\[\Rightarrow {{y}^{2}}+6y+34={{y}^{2}}-12y+52\]
We can now simplify the above step, we get
\[\begin{align}
  & \Rightarrow 18y=18 \\
 & \Rightarrow y=1 \\
\end{align}\]
We can now substitute the value of y in (3), we get
AQ = \[\sqrt{16+1+36-12}=\sqrt{41}\].
Therefore, the value of y is 1 and the distance between AQ is \[\sqrt{41}\] square units.

Note: Students make mistakes while assigning the points in the distance formula. We should remember the distance formula to find the distance. We should also remember that, Since \[A\left( 3,y \right)\] is equidistant from points \[P\left( 8,-3 \right)\] and \[Q\left( 7,6 \right)\],then AP will be equal to AQ.