Question

If $P\left( 2,2 \right),Q\left( -2,4 \right),R\left( 3,4 \right)$ are the vertices of a triangle $\Delta PQR$ then, the equation of the median through the vertex $R$ is:
(a) $x+3y-9=0$
(b) $x-3y+9=0$
(c) $x-3y-9=0$
(d) $x+3y+9=0$

Answer 1

Hint: We solve this problem by using the condition that the median through a vertex cuts the opposite side into two equal parts. We find the mid – point of $PQ$ and find the equation of the line passing through $R$ and the mid – point of $PQ$ which is the required answer.
The mid – point of $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as,
$\Rightarrow M=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
The equation of line passing through the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as,
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Where, $'m'$ is the slope of the line given as, $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$

Complete step by step solution:

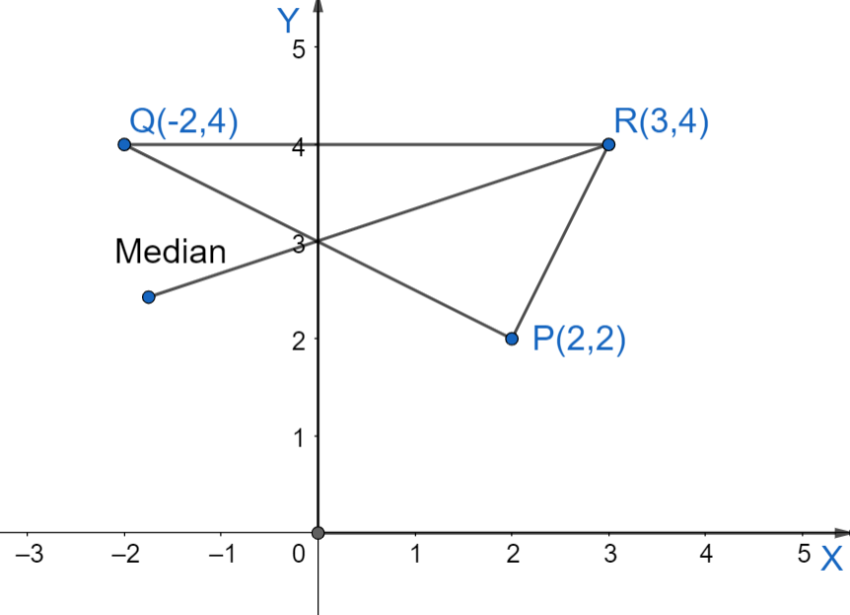
We are given that the coordinates of vertices of triangle $\Delta PQR$ as $P\left( 2,2 \right),Q\left( -2,4 \right),R\left( 3,4 \right)$
We are asked to find the median through the vertex $R$
We know that the median from the vertex cuts the opposite side into two equal parts.
Let us find the mid – point of $PQ$
We know that the mid – point formula of any two points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as,
$\Rightarrow M=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
By using this formula to vertices $P,Q$ then we get the mid – point $D$ as,
$\begin{align}
  & \Rightarrow D=\left( \dfrac{2+\left( -2 \right)}{2},\dfrac{2+4}{2} \right) \\
 & \Rightarrow D=\left( 0,3 \right) \\
\end{align}$
Now, let us find the slope of the line $DP$
We know that the slope of line passing through two points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
By using this formula to the points $D\left( 0,3 \right),R\left( 3,4 \right)$ then we get the slope of $DP$as,
$\begin{align}
  & \Rightarrow m=\dfrac{4-3}{3-0} \\
 & \Rightarrow m=\dfrac{1}{3} \\
\end{align}$
Now, let us find the equation of line $DP$
We know that the equation of line passing through the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as,
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Where, $'m'$ is the slope of the line.
By using this standard equation of line we get the required equation of $DP$ as,
$\begin{align}
  & \Rightarrow y-3=\dfrac{1}{3}\left( x-0 \right) \\
 & \Rightarrow 3y-9=x \\
 & \Rightarrow x-3y+9=0 \\
\end{align}$
Therefore, we can conclude that the required equation of median of given triangle $\Delta PQR$ through vertex $R$ is given as,
$\therefore x-3y+9=0$
So, the correct answer is “Option A”.

Note: We need to note that through which vertex the median is required. The median passing through a vertex intersects the opposite side at mid – point. Here, the required median passes through the vertex $R$ so that the median touches $PQ$ at its mid – point.
Some students may make mistakes by taking the mid – point of either $PR$ or $QR$ which result in wrong answers. We need to take the mid – point of the opposite side of the required vertex.