Question

If $PL, QM$ and $RN$ are the altitudes of triangle $PQR$ whose orthocentre is $O$, then $Q$ is the orthocentre of the triangle
A. $OPQ$
B. $OQR$
C. $PLR$
D. $OPR$

Answer 1

Hint:
From the definition of orthocentre, it is the meeting point of the altitudes of the triangle. Then, $PL \bot QR$, $QM \bot PR$ and $RN \bot PQ$.Draw a corresponding figure. Next, find the triangle whose altitudes of all vertices meet at point $Q$ and that triangle will be the required answer.

Complete step by step solution:
We are given that $PL,QM$ and $RN$ are the altitudes of triangle $PQR$
This implies, $PL \bot QR$, $QM \bot PR$ and $RN \bot PQ$
Also, we have been given that the orthocentre of triangle $PQR$ is $O$.

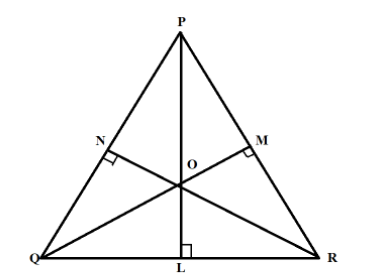
Here, we can see that $QM \bot PR$
Also, triangle $POR$ will be an obtuse triangle and its orthocentre will lie outside the triangle.
The line $OR$ we have the perpendicular $QR$ outside the triangle.
And for the line $OP$ we have the perpendicular $QP$ outside the triangle.
And all the altitudes of triangle $POR$ meet at $Q$, then the orthocentre of $POR$ is $Q$.

Hence, option D is correct.

Note:
If we draw a triangle from any of the four points, that are the vertices and the orthocentre of that triangle, $P,Q,R,O$, then the fourth point has to be orthocentre. If \[Q\] has to be the orthocentre, then the corresponding triangle will be $POR$.