Question

If PA and PB are tangents to a circle with centre O. If $ \angle APB={{\left( 2x+3 \right)}^{{}^\circ }} $ and \[\angle AOB={{\left( 3x+7 \right)}^{{}^\circ }}\] then find the value of x.

Answer 1

Hint: The four sided closed figure is called the quadrilateral. Tangent cut the circle or any surface only once as it never crosses the perimeter of a figure. In quadrilateral, sum of all angles is equals to $ {{360}^{{}^\circ }} $ and sum of opposite sides are equals to $ {{180}^{{}^\circ }} $ . Here, we will use the concept of the sum of two opposite angles in quadrilateral AOBP.

Complete step-by-step answer:

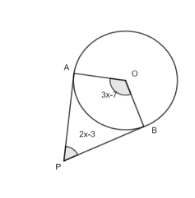
Now, in the given figure we have a circle with centre O. we have two tangents namely PA and PB. Also, OA = OB as both are equal to the radius of the circle. Its is given that $ \angle APB={{\left( 2x+3 \right)}^{{}^\circ }} $ and \[\angle AOB={{\left( 3x+7 \right)}^{{}^\circ }}\].
Now, in figure we can see that there is a quadrilateral AOBP. And, in quadrilateral AOBP, \[\angle AOB\] and $ \angle APB $ are opposite angles.
 In a four sided figure which is called quadrilateral, sum of all angles is equals to $ {{360}^{{}^\circ }} $ and sum of opposite sides are equals to $ {{180}^{{}^\circ }} $ .
So, as from data given in question, $ \angle APB={{\left( 2x+3 \right)}^{{}^\circ }} $ and \[\angle AOB={{\left( 3x+7 \right)}^{{}^\circ }}\]also from figure we can see that angles \[\angle AOB\] and \[\angle APB\] both are opposite angles in quadrilateral AOBP.
So, \[\angle AOB+\angle APB={{180}^{{}^\circ }}\] …… ( i )
Substituting values of \[\angle AOB\] and \[\angle APB\] in equation ( i ), we get
 $ {{\left( 2x+3x+3+7 \right)}^{{}^\circ }}={{180}^{{}^\circ }} $ $ {{\left( 2x+3 \right)}^{{}^\circ }}+{{\left( 3x+7 \right)}^{{}^\circ }}={{180}^{{}^\circ }} $ .
Collecting like terms together,
 $ {{\left( 2x+3x+3+7 \right)}^{{}^\circ }}={{180}^{{}^\circ }} $ .
Adding like terms together ,
 $ {{\left( 5x+10 \right)}^{{}^\circ }}={{180}^{{}^\circ }} $ .
Moving 10 from left hand side to right hand side, we get
\[{{\left( 5x \right)}^{{}^\circ }}={{180}^{{}^\circ }}-{{10}^{{}^\circ }}\] .
Subtracting 10 from 180, we get
\[{{\left( 5x \right)}^{{}^\circ }}={{170}^{{}^\circ }}\] .
Dividing both side by 5, we get
\[{{\left( \dfrac{5x}{5} \right)}^{{}^\circ }}={{\dfrac{170}{5}}^{{}^\circ }}\] .
Simplifying both sides, we get
\[x={{34}^{{}^\circ }}\] .
Hence, the value of x is equals to $ {{34}^{{}^\circ }} $ .

Note: Always remember that in quadrilateral, sum of all angles is equals to $ {{360}^{{}^\circ }} $ and sum of opposite sides are equals to $ {{180}^{{}^\circ }} $ . Two angles facing each other are called opposite angles. While writing the answers the sign of degree must be placed at last. Here, calculation mistakes may occur, so calculation must be done very precisely and accurately.