Question

If \[{P_1},{P_2},{P_3}\] are the perpendiculars from the vertices of a triangle to the opposite side then \[{P_1}{P_2}{P_3}\] is equal to
A. \[{a^2}{b^2}{c^2}\]
B. \[2{a^2}{b^2}{c^2}\]
C. \[\dfrac{{4{a^2}{b^2}{c^3}}}{{{R^2}}}\]
D. \[\dfrac{{{a^2}{b^2}{c^2}}}{{8{R^3}}}\]

Answer 1

Hint: This question needs a figure that will show the perpendiculars, the sides of the triangle and the whole scenario will be cleared. We will use the formula for finding the area of the triangle to get nearer to the answer. We will refer to the area of the triangle to be \[\Delta \]. Then we will convert them in the form of the perpendiculars. After that the product of the equations will be the answer.

Complete step by step solution:
First we will draw \[\vartriangle ABC\]. That triangle with perpendiculars \[{P_1},{P_2},{P_3}\] drawn from the vertex A, B and C on the sides BC, AC and AB respectively.

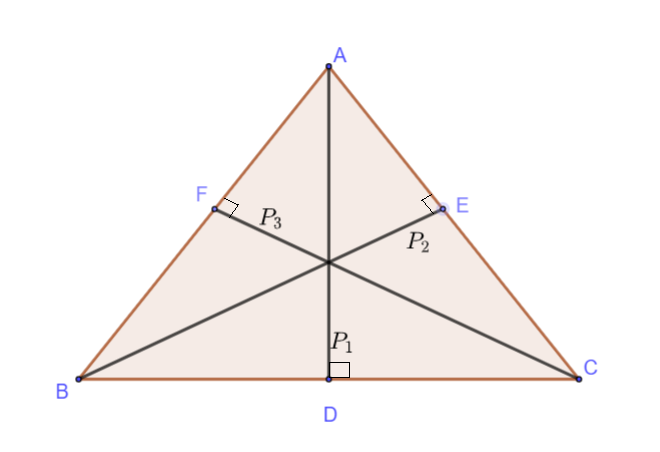
Now the picture of the problem is totally clear.
We know that,
\[A\left( {\vartriangle ABC} \right) = \dfrac{1}{2} \times base \times height\]
Let \[A\left( {\vartriangle ABC} \right) = \Delta \]
So we can write this in three different ways,
Consider the side opposite to vertex A as a, that opposite to vertex B as b and that opposite to vertex C as c.
Thus,
\[{\text{}}\Delta {\text{}} = \dfrac{1}{2} \times AD \times BC = \dfrac{1}{2} \times {P_1} \times a\]
\[{\text{}}\Delta = \dfrac{1}{2} \times BE \times AC = \dfrac{1}{2} \times {P_2} \times b{\text{\;}}\]
\[\Delta {\text{}} = \dfrac{1}{2} \times CF \times AB = \dfrac{1}{2} \times {P_3} \times c{\text{\;}}\]

These are the equations that can be drawn.
Now we will transpose the terms in such a way that they will be in the perpendiculars form.
\[{P_1} = \dfrac{{2\Delta }}{a},{P_2} = \dfrac{{2\Delta }}{b},{P_3} = \dfrac{{2\Delta }}{c}\]
Now taking the product of these three we get,
\[{P_1}{P_2}{P_3} = \dfrac{{8{\Delta ^3}}}{{abc}}\]
As we know that, \[\Delta = \dfrac{{abc}}{{4R}}\]
Now using this data in the above formula we can replace \[\Delta \] as,
 \[{P_1}{P_2}{P_3} = \dfrac{{8{{\left( {\dfrac{{abc}}{{4R}}} \right)}^3}}}{{abc}}\]
Now we can shift the denominator as,
\[{P_1}{P_2}{P_3} = \dfrac{{8{{\left( {abc} \right)}^3}}}{{{{\left( {4R} \right)}^3}abc}}\]
\[{P_1}{P_2}{P_3} = \dfrac{{8{{\left( {abc} \right)}^3}}}{{64{R^3}abc}}\]
Cancelling abc and dividing 64 by 8 we get,
\[{P_1}{P_2}{P_3} = \dfrac{{{{\left( {abc} \right)}^2}}}{{8{R^3}}}\]
This is simplified as,
\[{P_1}{P_2}{P_3} = \dfrac{{{a^2}{b^2}{c^2}}}{{8{R^3}}}\]

So, the correct answer is “Option D”.

Note: Here note that the letter R used in option C and D is the concept of circumradius that is inscribed in circumcircle. A circle that is inscribed in a triangle. Also note that if \[\Delta \] is not replaced then the answer might be different. But we have to replace it because in option \[\Delta \] is not available. So we took help of circumradius concept.