Question

If \[P = \left( {x,y} \right),{F_1} = \left( {3,0} \right), {F_2} = \left( { - 3,0} \right)\] and \[16{x^2} + 25{y^2} = 400\], then find the value of \[P{F_1} + P{F_2}\].
A) 8
B) 6
C) 10
D) 12

Answer 1

Hint: First we want to find the nature of the given equation like the geometrical shape which it forms. It can a be a ellipse, circle or a hyperbola. After getting the nature of the given equation, we will proceed accordingly.

Complete step by step solution:
Consider the given equation \[16{x^2} + 25{y^2} = 400\]
We divide the equations on both sides by 400
 \[
   \Rightarrow \dfrac{{16{x^2} + 25{y^2}}}{{400}} = \dfrac{{400}}{{400}} \\
    \\
 \]
Now we are going to split the denominator of left hand side term.
\[
   \Rightarrow \dfrac{{16{x^2}}}{{400}} + \dfrac{{25{y^2}}}{{400}} = 1 \\
   \Rightarrow \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1 \\
 \]
The equation \[\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\]is of the form of \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] which is the equation of ellipse.
So \[\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\] is equation of ellipse.
Here \[{a^2} = 25,{b^2} = 16\]
Where $a$ is the measure of the semi axis of the ellipse which lies on the X-axis and b is the measure of the semi axis of the ellipse which lies on the Y-axis.
Now we are going to find foci of the ellipse by using a formula.
We know that \[{b^2} = {a^2}\left( {1 - {e^2}} \right)\]
Now let us put the value of ‘a’ and ‘b’ in the above equation then we get the eccentricity of the ellipse.
\[ \Rightarrow 16 = 25\left( {1 - {e^2}} \right)\]
Now we are going to find the value of ‘e’ so that we will keep numbers on one side and ‘e’ on one side.\[
  \dfrac{{16}}{{25}} = 1 - {e^2} \\
    \\
 \]
\[
   \Rightarrow 1 - \dfrac{{16}}{{25}} = {e^2} \\
    \\
 \]
Now we are going to take LCM then proceed.
\[
   \Rightarrow {e^2} = \dfrac{{25 - 16}}{{25}} \\
   \Rightarrow {e^2} = \dfrac{9}{{25}} \\
    \\
 \]
Now we are going to take square root on both sides, then we get the value of ‘e’
\[e = \dfrac{3}{5}\]
Now we are going to find the value of$ae$to determine the foci of the given ellipse.
$
  ae = 5 \times \dfrac{3}{5} \\
  ae = 3{\text{ }} \\
 $ (Cancelling 5 in both numerator and denominator)
Now we are going to find foci of the ellipse.
Now, foci of the ellipse are \[\left( { \pm ae,0} \right) = \left( { \pm 3,0} \right)\]
The foci of the given ellipse are \[{F_1} = ( + 3,0)\] and \[{F_2} = ( - 3,0)\]
Now, we are going to find the value of \[P{F_1} + P{F_2}\]
By the properties of ellipse, we know that if $P(x,y)$ is a generic point on ellipse and \[{F_1}\] and \[{F_2}\] are foci of the ellipse then the sum of the distances of $P$ from the two fixed points \[{F_1}\] and \[{F_2}\]equals to $2a$.

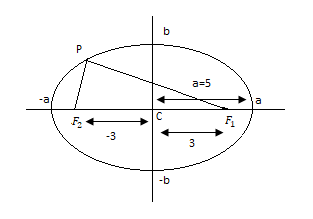
$\therefore $ \[ \Rightarrow P{F_1} + P{F_2} = 2a{\text{ = 2}} \times {\text{5 = 10}}\]

Note:
First, we need to be careful while solving the given equation. Then we have to determine the nature of the equation whether the equation is of parabola, hyperbola, and ellipse. After finding the nature of the given equation, we have to proceed and use the properties and formulae of the nature of the equation to attain the solution.