Question

If P is any point on the ellipse \[(\dfrac{{{x^2}}}{{36}}) + (\dfrac{{{y^2}}}{{16}}) = 1\]and\[\;S\] and \[S'\] are the foci, then \[PS{\text{ }} + {\text{ }}PS'{\text{ }} = \]
\[1)\]$4$
\[2)\]$8$
\[3)\]$10$
\[4)\]$12$

Answer 1

Hint: We have to find the value of sum of \[PS\] and \[PS'\] . We solve this question using the concept of an ellipse . We should have the knowledge about the terms such as foci , vertex point and the centre point of the ellipse . We use the formula of focal distance of any point P on the ellipse . We should also have the concept of length of major axis and minor axis .

Complete step-by-step solution:
Given :
\[(\dfrac{{{x^2}}}{{36}}) + (\dfrac{{{y^2}}}{{16}}) = 1\]
We know that the general equation of ellipse is given by :-
$\dfrac{{{{(x - h)}^2}}}{{{a^2}}} + \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1$
Where a and b are the length of major axis and minor axis respectively \[\left( {{\text{ }}a{\text{ }} > {\text{ }}b{\text{ }}} \right){\text{ }}.{\text{ }}\left( {h{\text{ }},{\text{ }}k} \right)\] are the centre point of the ellipse .
Comparing the two equations , we compute that ${a^2} = 36,{b^2} = 16,h = 0$ and \[k{\text{ }} = {\text{ }}0\] .
The centre point of the ellipse is \[\left( {0{\text{ }},{\text{ }}0} \right)\] .
The length of major axis \[ = {\text{ }}6{\text{ }}units\]
The length of minor axis \[ = {\text{ }}4{\text{ }}units\]
Point of foci of an ellipse is \[\left( {{\text{ }} \pm {\text{ }}c{\text{ }},{\text{ }}0{\text{ }}} \right)\]
The formula for calculating the foci is $c = \sqrt {[{a^2} - {b^2}]} $
The point of foci of the ellipse $ = ( \pm \sqrt {[36 - 16]} ,0)$
The point of foci of the ellipse $ = ( \pm 2\sqrt 5 ,0)$
The sum of distance of a point P on the ellipse from the foci is equal to twice the length of the major axis .
So ,
\[PS{\text{ }} + {\text{ }}PS'{\text{ }} = {\text{ }}2{\text{ }} \times {\text{ }}6\]
\[PS{\text{ }} + {\text{ }}PS'{\text{ }} = {\text{ }}12{\text{ }}units\]
Thus , the sum of distance of point $P$ from the foci $S$ and $S'$ is \[12{\text{ }}units\] .
Hence , the correct option is \[\left( 4 \right)\]

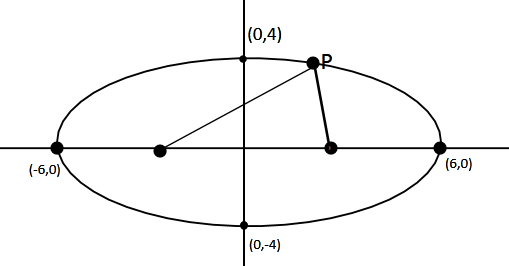
Note: An ellipse is the set of all points in a plane , the sum of whose distance from two fixed points in the plane is a constant . The Latus Rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose endpoints lie on the ellipse . Length of the Latus Rectum of the ellipse $(\dfrac{{{x^2}}}{{{a^2}}}) + (\dfrac{{{y^2}}}{{{b^2}}}) = 1$ is $2 \times (\dfrac{{{b^2}}}{a})$ .