Question

If O is the origin and \[P({x_1},{y_1})\],\[Q({x_2},{y_2})\] are two points then \[OP \times OQ\sin \angle POQ = \]
A. \[{x_1}{x_2} + {y_1}{y_2}\]
B. \[{x_1}{y_2} + {x_2}{y_1}\]
C. \[{x_1}{y_2} - {x_2}{y_1}\]
D. None of these

Answer 1

Hint: We draw a rough diagram for the lines OP and OQ and use the formula of area of triangle formed by joining the three points O, P and Q. Calculate the area using matrix formula and area using the cross product formula. Equate the two equations obtained from the formula of area.
* Area of a triangle formed by points \[({x_1},{y_1}),({x_2},{y_2}),({x_3},{y_3})\]is given by \[\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\]
* Determinant of a matrix \[\left[ {\begin{array}{*{20}{c}}
  a&b&c \\
  d&e&f \\
  g&h&i
\end{array}} \right] = a(ei - hf) - b(di - fg) + c(dh - eg)\]
* Area of a triangle formed by the two sides \[AB\]and \[CD\]is given by \[\dfrac{1}{2}\left( {AB} \right)\left( {CD} \right)\sin \theta \], where \[\theta \]is the angle between the sides.

Step-By-Step answer:
We first draw a diagram for the lines OP and OQ

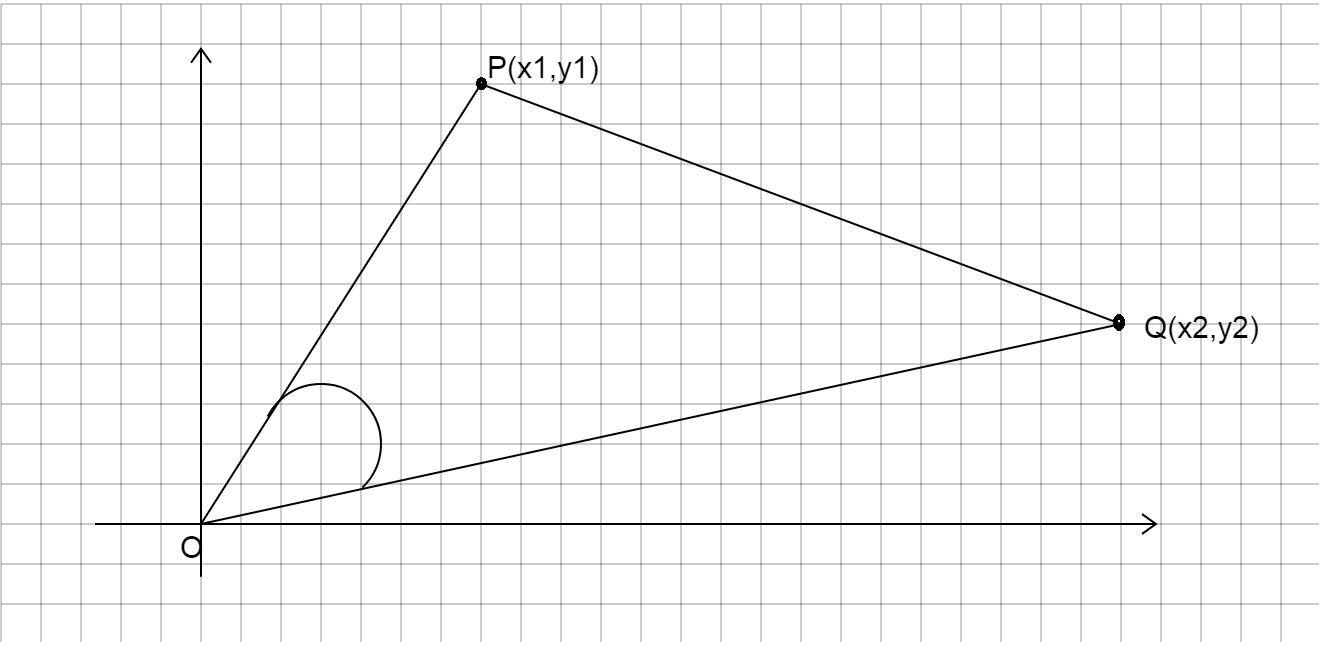
We are given three points \[O(0,0)\], \[P({x_1},{y_1})\]and \[Q({x_2},{y_2})\]
We can write the area of triangle formed by joining three points O, P and Q as
\[ \Rightarrow \]Area of triangle OPQ \[ = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  0&0&1
\end{array}} \right|\]
Calculate the determinant in RHS of the equation
Since determinant of a matrix \[\left[ {\begin{array}{*{20}{c}}
  a&b&c \\
  d&e&f \\
  g&h&i
\end{array}} \right] = a(ei - hf) - b(di - fg) + c(dh - eg)\]
\[ \Rightarrow \]Area of triangle OPQ \[ = \dfrac{1}{2}\left[ {{x_1}({y_2}) - {y_1}({x_2})} \right]\] … (1)
Now we calculate the area of triangle OPQ using length of sides formula
Since angle between the sides OP and OQ is \[\angle POQ,\]
We can write area of triangle OPQ \[ = \dfrac{1}{2}\left( {OP} \right)\left( {OQ} \right)\sin \angle POQ\] … (2)
Equate the area obtained from both equations (1) and (2)
\[ \Rightarrow \dfrac{1}{2}\left[ {{x_1}({y_2}) - {y_1}({x_2})} \right] = \dfrac{1}{2}\left( {OP} \right) \times \left( {OQ} \right)\sin \angle POQ\]
Cancel same factors from both sides of the equations
\[ \Rightarrow \left[ {{x_1}{y_2} - {y_1}{x_2}} \right] = OP \times OQ\sin \angle POQ\]

\[\therefore \]Option D is correct.

Note: Many students make mistake of assuming or writing the second formula of area of triangle as cross product or area of triangle made by vectors, keep in mind here we are not given any vectors, the formula states the area of triangle formed by two sides having one common vertex is given by the formula, do not mistake this formula with vector formula.