Question

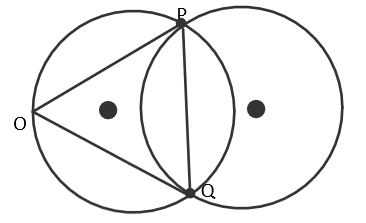
If O is the origin and OP, OQ are distinct tangents to circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$,
the circumcentre of the triangle OPQ is
(a) (-g, -f)
(b) (g, -f)
(c) (-f, -g)
(d) None of these

Answer 1

Hint: Here, we will first write the equation of the chord of contact, that is, PQ. Then, we will write the
equation of circle which passes through the intersection of the given circle and the chord of contact.
Using this equation, we will find the centre of the circle so obtained. The centre of circle
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is given as (-g, -f).

Complete step-by-step solution -
The chord joining the points of contact of the two tangents to a conic drawn from a given point, outside
it is called the chord of contact of the tangents. For a circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$, chord of
contact is given as $x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}$ and for a general circle, it is given as
$x{{x}_{1}}+y{{y}_{1}}+g\left( {{x}_{1}}+x \right)+f\left( {{y}_{1}}+y \right)+c=0$.
Since, PQ is the chord of contact of the tangents from the origin O to the
circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0........\left( 1 \right)$
So, the equation of PQ is given as $gx+fy+c=0......\left( 2 \right)$, ( because the chord of contact is drawn
from (0, 0) and so ${{x}_{1}}={{y}_{1}}=0$)

An equation of a circle through the intersection of (1) and (2) is given by:
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c+\lambda \left( gx+fy+c \right)=0........\left( 3 \right)$
Or, ${{x}^{2}}+{{y}^{2}}+gx\left( 2+\lambda \right)+fy\left( 2+\lambda \right)+c\left( 1+\lambda
\right)=0$
Since, the circle representing equation (3) passes through origin, the constant term must be zero.
Therefore, $c\left( 1+\lambda \right)=0$ which means c = 0 or $1+\lambda =0$.
$1+\lambda =0\Rightarrow \lambda =-1$
On putting $\lambda =-1$ in equation (1), we get:
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c+\left( -1 \right)\left( gx+fy+c \right)=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c-gx-fy-c=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}+gx+fy=0.........\left( 4 \right) \\
\end{align}$
So, this is the equation of the circumcircle of triangle OPQ.
Therefore, the circumcentre is given as the centre of the circle representing equation (4).
Thus, the circumcentre is $\left( \dfrac{-g}{2},\dfrac{-f}{2} \right)$.
Hence, option (d) is the correct answer.

Note: Students should note here that the centre of a circle is always given as $\left( \left( \dfrac{-1}{2}\times \text{coefficient of x} \right),\left( \dfrac{-1}{2}\times \text{coefficient of y} \right) \right)$. So, the calculations should be done accordingly, It should be kept in mind that the circumcentre of a triangle is the centre of its circumcentre. We cannot use the concept of intersection of its bisectors in this problem.