Question

If O is the centre of the circle and $\angle ADC={{140}^{\circ }}$, then what is the value of $x$?

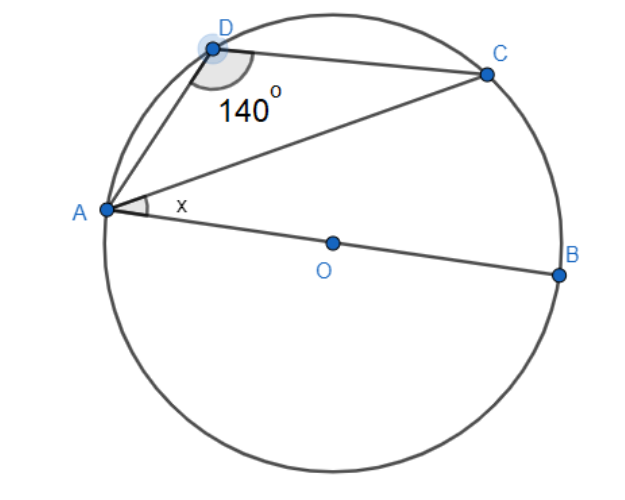
A. ${{35}^{\circ }}$
B. ${{55}^{\circ }}$
C. ${{60}^{\circ }}$
D. ${{50}^{\circ }}$

Answer 1

Hint: We first get the formula of centred angle for the same arc as double of the inscribed angle. We find that the centred angle for greater angle $\angle AOC$. We also use the equality of the radii to find the variable angle of $x$.

Complete step-by-step answer:
We first join the points O and C.

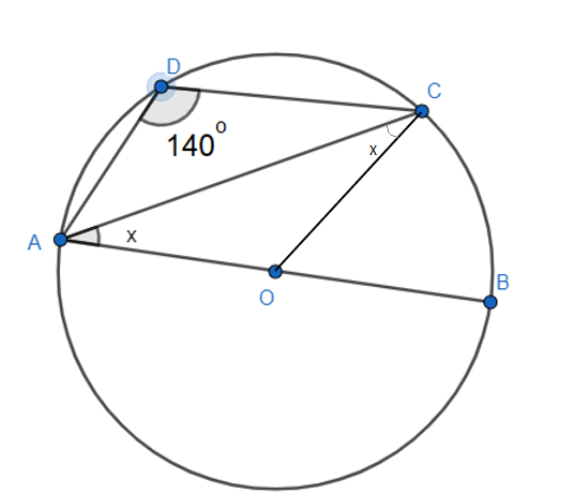
We know that the centred angle for the same arc is double of the inscribed angle.
We take the greater arc form of $\overset\frown{AC}$. The inscribed angle is $\angle ADC={{140}^{\circ }}$ and the central angle is greater angle $\angle AOC$.
Therefore, $\angle AOC=2\times \angle ADC=2\times {{140}^{\circ }}={{280}^{\circ }}$.
The total angle around point O is ${{360}^{\circ }}$.
Therefore, smaller $\angle AOC={{360}^{\circ }}-{{280}^{\circ }}={{80}^{\circ }}$.
In $\Delta AOC$, we have $\angle AOC+\angle OAC+\angle OCA={{180}^{\circ }}$.
We get $\angle AOC={{360}^{\circ }}-{{280}^{\circ }}={{80}^{\circ }}$.
Therefore, $\angle OAC+\angle OCA={{180}^{\circ }}-{{80}^{\circ }}={{100}^{\circ }}$.
We have two radii $AO=OC$. Therefore, in $\Delta AOC$, we get $\angle OAC=\angle OCA$.
As both are equal, we get $\angle OAC=\angle OCA=x=\dfrac{{{100}^{\circ }}}{2}={{50}^{\circ }}$.
The correct option is D.
So, the correct answer is “Option D”.

Note: We have to be careful about the arc difference for greater and smaller ones. The change of arc for the circle creates different angle relations. We have to also consider the direct proportional relation for the arc and the respective angle.