Question

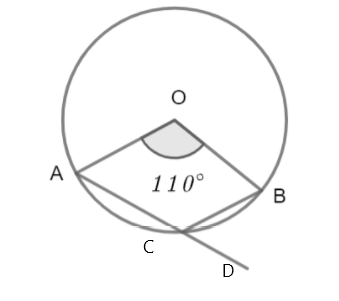
If O is the centre of a circle as shown in the figure and \[\angle AOB={{110}^{\circ }}\]. Find \[\angle BCD\].

Answer 1

Hint: In order to find the measure of \[\angle BCD\], we will be finding the reflex of \[\angle AOB={{110}^{\circ }}\] first. Then we will be applying the property of supplementary angles to the angles \[\angle BCD\] and\[\angle ACB\]. We will be substituting the known angle values and solving it for the angle \[\angle BCD\]. This measure of \[\angle BCD\] is our required answer.

Complete step by step answer:
Now let us learn about supplementary angles. Supplementary angles are those angles whose measure is \[{{180}^{\circ }}\]. If two supplementary angles join together, it forms a straight line and a straight line. It is not necessary that the angles should be next to each other or joined together. In a pair of supplementary angles, one of the angles would be obtuse angle and the other would be acute angle. There are several other types of pairs of angles such as complementary angles, linear pair of angles, alternate angles, vertically opposite angles, etc.
Now let us find the measure of \[\angle BCD\].
We are given that \[\angle AOB={{110}^{\circ }}\]
Now let us find the reflex of \[\angle AOB\]
\[\Rightarrow 360-110=250\]
We can say that \[\angle ACB=\] \[\dfrac{1}{2}\times \]reflex of \[\angle AOB\], because the angle subtended by arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
\[\Rightarrow \dfrac{1}{2}\times 250=125\]
\[\angle ACB={{125}^{\circ }}\]
Now, we can apply the property of supplementary angles to \[\angle BCD\] and\[\angle ACB\].
\[\begin{align}
  & \angle BCD+\angle ACB=180 \\
 & \Rightarrow \angle BCD+125=180 \\
 & \Rightarrow \angle BCD=180-125=55 \\
\end{align}\]
\[\therefore \angle BCD={{55}^{\circ }}\]

Note: While solving such problems regarding angles, we must check for the properties of angles that can be applied so that our solving would become easier. We can also observe that the quadrilateral in the circle forms a cyclic quadrilateral. We found the angle \[\angle ACB\] as it forms one of the supplements of the angles.