Question

If 'O' is at equilibrium then the values of the tension T$_1$ and T$_2$ are (20 N is acting vertically downwards at O).

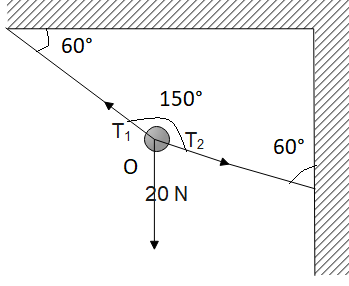
(A) 20 N, 30 N
(B) 20$\sqrt{3}$ N, 20 N
(C) 20$\sqrt{3}$ N, 20$\sqrt{3}$ N
(D) 10 N, 30 N

Answer 1

Hint: In the figure, it can be clearly seen that an equilibrium of the forces have been established. The ball is at the balance point so the vertical and horizontal components of the forces can be equated to provide us two equations for two variables.
Formula Used:
The sum of all the forces on a body in equilibrium is zero:
${\vec F_1} + {\vec F_2} + {\vec F_3} + ... = 0$.
These forces are to be written in the component form and the same equation applies to both x and y (or horizontal or vertical) components.

Complete answer:
Consider the following diagram:

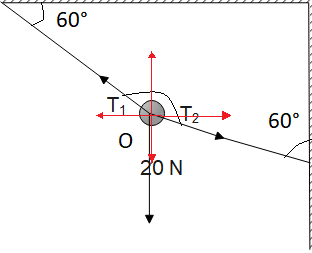
Looking at the arrows, we can get an idea about the direction of the forces. Two red lines have been drawn to mark the direction of the horizontal and the vertical axis.
First let us consider the vertical components, the downwards forces and upwards force components and upon balancing these components, we will get:
$\eqalign{
  & {T_1}\cos 30^\circ = {T_2}\sin 30^\circ + 20{\rm{ N}} \cr
  & \Rightarrow {T_1}\sqrt 3 = {T_2} + 40 \cr} $
Now, if we consider the horizontal components and we balance those, we get:
$\eqalign{
  & {T_1}\sin 30^\circ = {T_2}\cos 30^\circ \cr
  & \Rightarrow {T_1} = {T_2}\sqrt 3 \cr} $
Keeping this in the previous equation:
$\eqalign{
  & \therefore 3{T_2} = {T_2} + 40 \cr
  & \Rightarrow {T_2} = 20{\text{ N}}{\text{.}} \cr} $
Keeping this value in the equation for T$_1$, we get:
${T_1} = 20\sqrt 3 $N.

Therefore, from the given set of options, the correct answer is option (B).

Note:
To obtain the angles that the vectors make with the horizontal components, we just took the right angled triangles that were forming with the string and the directions. For example, to get what angle the vector T$_1$ makes with the vertical (upwards) direction, we just could extend our red line further up and form a right angled triangle. The required angle plus the given angle (question diagram) should make a right angle.