Question

If o is a point within quadrilateral $$ABCD$$ , show that $$OA + OB + OC + OD > AC + BD$$

Answer 1

Hint: We need to draw quadrilateral and do Construction as Join $$OA,OB,OC\;and\;OD$$ . Also, join $$AC\;and\;BD$$ after comparing the triangles inside quadrilaterals, we can prove the given statement.

Complete step-by-step answer:
Given that $$ABCD$$ is a quadrilateral. O is a point inside the quadrilateral $$ABCD$$ .
 We have to prove $$OA + OB + OC + OD > AC + BD$$
Let draw quadrilateral and do Construction as Join $$OA,OB,OC\;and\;OD$$ . Also, join $$AC\;and\;BD$$ .

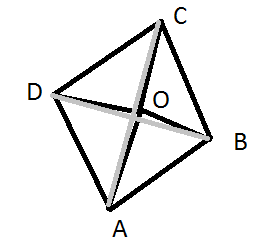
So As we know that the sum of any two sides of a triangle is greater than the third side.
 Therefore,
In $$\vartriangle BOD,OB + OD > BD$$ .....(1)
 Similarly
In △ $$AOC,OA + OC > AC$$.....(2)
 Adding eqn(1)&(2), we have
   $OB + OD + OA + OC > BD + AC$
   $\Rightarrow$ $OA + OB + OC + OD > AC + BD$
Hence proved

Note: Here we had to prove $$OA + OB + OC + OD > AC + BD$$ all we did is we drew quadrilateral and did Construction as Join $$OA,OB,OC\;and\;OD$$ . Also, join $$AC\;and\;BD$$. After we compare triangles inside the quadrilateral, and do prove the statement. Construction is required to solve these types of questions.