Question

If n(A) = 7, n(B) = 9 and \[n\left( A\cup B \right)=14\], then what is the value of \[n\left( A\cap B \right)\].

Answer 1

Hint: First of all try to recollect the various terminologies related to sets like the union of sets, the intersection of sets, etc. Now use the formula for the union of two sets that is \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]. Here, substitute the given values to find the value of \[n\left( A\cap B \right)\].

Complete step-by-step answer:
Before proceeding with the question, let us understand the terminologies of sets.
Sets: Set is basically a collection of well-defined and distinct objects considered as an object in its own right. n (A) signifies the number of elements in set A
 

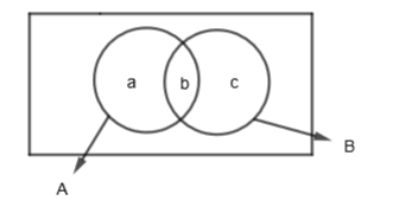
In the above Venn Diagram, region (a + b) gives set A and region (b + c) gives set B
Union of two sets \[\left( \cup \right)\]: The union of two sets is a new set that contains all the elements that are in at least one of the two sets.

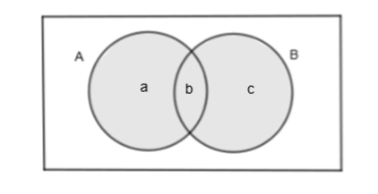
In the above diagram, the shaded portion is \[\left( A\cup B \right)\text{ and }n\left( A\cup B \right)=a+b+c\].
The intersection of two sets\[\left( \cap \right)\]: The intersection of two sets is a set that contains all the elements that are in both sets.

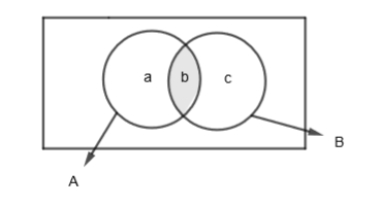
In the above diagram, the shaded portion is \[\left( A\cap B \right)\text{ and }n\left( A\cap B \right)=b\].
Hence, we can say that
\[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]
Now, let us consider our question. We are given that,
\[n\left( A \right)=7;n\left( B \right)=9;n\left( A\cap B \right)=14\]
Let us find the value of \[n\left( A\cap B \right)\] by using the above values. We know that, according to the theory of sets, the number of elements in the union of two sets is given by
\[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]
By substituting the values of \[n\left( A \right)=7;n\left( B \right)=9;n\left( A\cap B \right)=14\] in the above equation, we get,
\[14=7+9-n\left( A\cap B \right)\]
\[14=16-n\left( A\cap B \right)\]
\[n\left( A\cap B \right)=16-14\]
\[n\left( A\cap B \right)=2\]
Hence, we get the value of \[n\left( A\cap B \right)\text{ as }2\].
We can also represent the above situation by using a Venn diagram.


Note: Students can also solve the above question by using a Venn Diagram as follows:

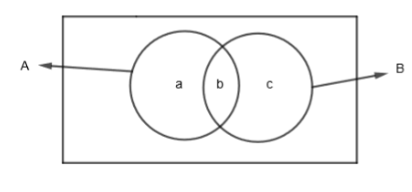
In the above diagram, we have taken 3 different regions with names a, b and c. Here,
\[A=a+b;B=b+c;\left( A\cup B \right)=a+b+c;\left( A\cap B \right)=b\]
We are given that,
n (A) = a + b = 7…..(i)
n (B) = b + c = 9…..(ii)
By adding equation (i) and (ii), we get,
a + b + b + c = 7 + 9
We also know that \[n\left( A\cup B \right)=a+b+c=14\]. By using this, we get,
14 + b = 16
b = 16 – 14 = 2 which is \[n\left( A\cap B \right)\].