Question

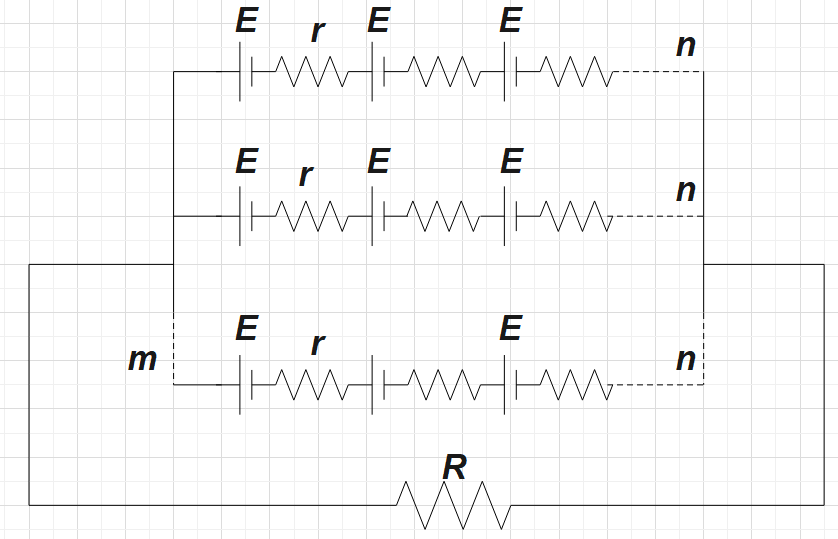
If n batches of m cells in series are connected in parallel with an external resistance R, then what is the expression for current I through R.

Answer 1

Hint: As a first step, read the question well and then analyse the given circuit. Then one could recall the expression for effective resistance and effective emf for series and parallel connections. Now, apply ohm’s law to get the current across the external resistor.

Formula used:
Effective resistance:
Series,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}+...$
Parallel,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+...$


Complete step by step solution:
In the question, we are given n batches of m cells connected in parallel with an external resistance of R. We are supposed to find the expression for current I through resistance R.
Though the circuit may scare you at the very first glimpse, this is a pretty easy question.
Firstly, let us consider only one of the branches in which n cells are connected in series. We know that net emf when n cells are connected in series would be given by $nE$. Similarly, the net internal resistance would be given by $nr$.
Now, you may see that we have m branches of $nr$resistance connected in parallel, the equivalent resistance here would be given by,
$\dfrac{1}{{{r}_{eq}}}=\dfrac{1}{nr}+\dfrac{1}{nr}+...=m\times \dfrac{1}{nr}$
$\Rightarrow {{r}_{eq}}=\dfrac{nr}{m}$……………………………………… (1)
Now we have the emf across the external resistance R to be given by $nE$. Now we could recall the ohm’s law,
$I=\dfrac{V}{R}$
$\therefore I=\dfrac{nE}{R+\dfrac{nr}{m}}$
Therefore, we found the expression for the current through the resistor R to be,
$I=\dfrac{nE}{R+\dfrac{nr}{m}}$

Note: One may recall that the emf across two points would remain the same as it is just a point dependent quantity. That is why we have taken the net emf of the combination of cells to $nE$. So, the m number of branches doesn’t affect the effective emf across the external resistor.