Question

If $m{x^2} - 9mx + 5m + 1 > 0\forall X \in R$, then $m$ lies in which interval?
A) $\left( { - \dfrac{4}{{61}},0} \right)$
B) $\left( {0,\dfrac{4}{{61}}} \right)$
C) $\left( {\dfrac{4}{{61}},\dfrac{{61}}{4}} \right)$
D) $\left( {\dfrac{{ - 61}}{4},0} \right)$

Answer 1

Hint: In this question, we are given an equation in terms of $x$ and $m$, and we have been asked in which interval $m$ lies. Observe that the given equation is quadratic of the form: $a{x^2} + bx + c = 0$.
For the given equation to be greater than 0, identify the conditions and fulfill them by putting the values and using formulae.

Complete step-by-step answer:
We have been given an equation: $m{x^2} - 9mx + 5m + 1 > 0\forall X \in R$ and we have been asked the interval within which $m$ lies.
If we observe properly, the given equation is a quadratic equation of the form: $a{x^2} + bx + c = 0$, where $a = m$, $b = - 9m$ and $c = 5m + 1$.
For our equation to be greater than 0, we need to follow certain conditions:
$a > 0$, and D (determinant) $ < 0$
We know that $D = {b^2} - 4ac$, and as per the condition, $d < 0$. Let us put the values in the formula:
$ \Rightarrow {\left( { - 9m} \right)^2} - 4m\left( {5m + 1} \right) < 0$
On simplifying we get,
$ \Rightarrow 81{m^2} - 20{m^2} - 4m < 0$
$ \Rightarrow 61{m^2} - 4m < 0$
Taking $m$ common,
$ \Rightarrow m(61m - 4) < 0$
$ \Rightarrow m = 0,\dfrac{4}{{61}}$
Now, we have two values of m. Let us plot them on the number line and use a wavy curve method. In this method, we start marking each interval as positive, negative, starting from making the right most interval as positive, next as negative and so on… It is done in the following way:

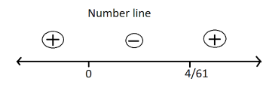
Now since we want our D to be negative, we will choose the interval $\left( {0,\dfrac{4}{{61}}} \right)$ as it is negative.

Hence, our correct option is option (B) $\left( {0,\dfrac{4}{{61}}} \right)$.

Note: We could also solve the question by elimination method. By looking at our condition that $a > 0$, and in this case, $a = m$, we know that m can only be positive. By this, we can eliminate our options (A) and (D).
Now, we only have options (B) and (C). We can check both of them by putting the values in the equation. This is called a hit and trial method. This will help us in eliminating one option.