Question

If median $AM$ of a $\Delta ABC$ is $3.5cm$ and the median $PM$ of a $\Delta PQR$ is $4cm$. If the area of $\Delta ABC$ is $49c{{m}^{2}}$ then find the area of $\Delta PQR$.

Answer 1

Hint: To solve this question we need to have the knowledge of the relation between the area and the median of the triangle. The two Triangles given are similar. The concept used to find the area is that the ratio of the area of the two Triangle is equal to the square of the ratio of the medians of the two Triangle.

Complete step by step answer:
The question ask us to find the value of the $\Delta PQR$ when the area of the $\Delta ABC$ is given as$49c{{m}^{2}}$ and the median of the Triangles$\Delta ABC$ and $\Delta PQR$which is$AM$ and $PM$ respectively having length $3.5cm$ and $4cm$.

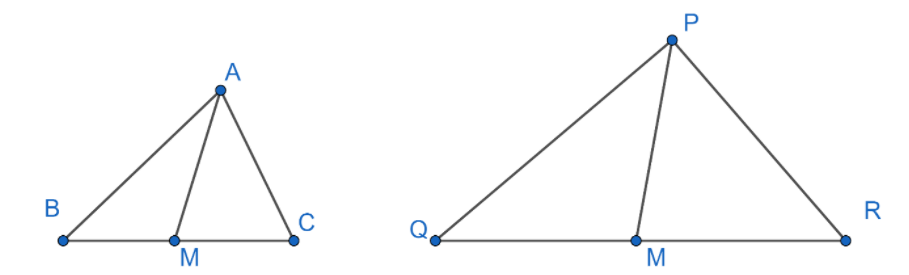We will use the concept that the ratio of the area of the two triangles is equal to the square of the median of the two triangles. On writing it mathematically the expression we get is:
\[\Rightarrow \dfrac{ar\Delta ABC}{ar\Delta PQR}={{\left( \dfrac{\text{median of }\Delta ABC}{\text{median of }\Delta PQR} \right)}^{2}}\]
We know that the median of the two triangles are given as $AM$ and $PM$. So we will substitute these values in the above equation.
\[\Rightarrow \dfrac{ar\Delta ABC}{ar\Delta PQR}={{\left( \dfrac{AM}{PM} \right)}^{2}}\]
We will substitute the values in the above expression as given in the question. On doing this we get:
\[\Rightarrow \dfrac{49}{ar\Delta PQR}={{\left( \dfrac{3.5}{4} \right)}^{2}}\]
On expanding the expression we get:
\[\Rightarrow \dfrac{49}{ar\Delta PQR}=\dfrac{3.5\times 3.5}{4\times 4}\]
We will cross multiply the term and take the unknown to one side and the known to the other side. On doing this we get:
\[\Rightarrow ar\Delta PQR=\dfrac{49\times 4\times 4}{3.5\times 3.5}\]
On solving the above expression we get:
\[\Rightarrow ar\Delta PQR=64c{{m}^{2}}\]
$\therefore $ The area of $\Delta PQR$ is $64c{{m}^{2}}$.

Note: The \[\dfrac{ar\Delta ABC}{ar\Delta PQR}={{\left( \dfrac{\text{median of }\Delta ABC}{\text{median of }\Delta PQR} \right)}^{2}}\], given concept will be used only if the triangles have certain similarity which means the triangles should be similar. In case the units given are different then we need to change all the dimensions into the same unit.