Question

If M and N are the midpoints of the diagonals AC and BD respectively of quadrilateral ABCD, then \[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = .....\]
A. $2\overline {MN} $
B. $2\overline {NM} $
C. $4\overline {MN} $
D. $4\overline {NM} $

Answer 1

Hint: In this question take a, b, c, d, m and n as the position vector of A, B, C, M and N also remember to use that $m = \dfrac{{a + c}}{2}$ and $n = \dfrac{{b + d}}{2}$, use this information to approach the solution.

Complete step-by-step answer:
According to the given information it is given that M and N are the midpoints of the diagonals AC and BD of a quadrilateral ABCD

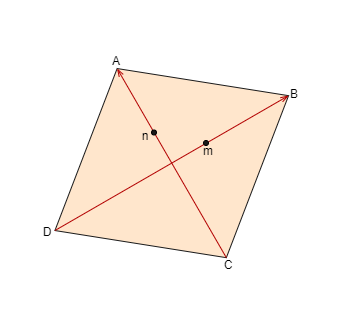
Let a, b, c, d, m, n be the position vectors of A, B, C, D, M and N respectively
Since it is given that M and N are the midpoint of diagonal AC and BD
Therefore, by midpoint formula we can say that $m = \dfrac{{a + c}}{2}$and $n = \dfrac{{b + d}}{2}$
2m = a + c and 2n = b + d
Now to find the value of \[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = .....\] let’s take this as equation 1
Let’s find the value of AB, AD, CB and CD
After using the concept of triangle law of vector addition we get
$ \Rightarrow $\[\overline {AB} = b - a\]
$ \Rightarrow $\[\overline {AD} = d - a\]
$ \Rightarrow $\[\overline {CB} = b - c\]
$ \Rightarrow $$\overline {CD} = d - c$
Now substituting the above values in the equation 1 we get
\[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = b - a + d - a + b - c + d - c\]
$ \Rightarrow $\[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = 2b - 2a - 2c + 2d\]
$ \Rightarrow $\[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = 2\left( {b + d} \right) - 2\left( {a + c} \right)\]
Now we know that 2m = a + c and 2n = b + d so after substituting the values in the above equation we get
\[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = 2\left( {2n} \right) - 2\left( {2m} \right)\]
$ \Rightarrow $\[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = 4\left( {n - m} \right)\]
Since we know that n – m is equal to vector $\overline {MN} $
Therefore, \[\overline {AB} + \overline {AD} + \overline {CB} + \overline {CD} = 4\overline {MN} \]

So, the correct answer is “Option C”.

Note: In the above solution we used the term “triangle law of vector addition” which can be explained as the pair of two vector which are represented by the two sides of the triangle and the third side of the triangle represents the resultant vector of both the vectors these two vectors are arranged in head to tail formation whereas the resultant vector is arranged in the opposite direction to the sequence of the vectors.