Question

If M and N are any two events, the probability that exactly one of them occurs is for an event set A, the complement is \[A^\circ \].
A. P( M ) + P( N ) – 2P( M\[ \cap \]N )
B. P( M ) + P( N ) – P( M\[ \cap \]N )
C. P( \[M^\circ \]) + P( \[N^\circ \]) – 2P(\[M^\circ \]\[ \cup \]\[N^\circ \])
D. P( M \[ \cap \]\[N^\circ \]) + P(\[M^\circ \]\[ \cup \] N )

Answer 1

Hint: M and N are the events of set A. In such a type of question the Venn diagram is the best way to understand the question properly so let us first of all draw a Venn diagram and then we will move on to solving the question.

Complete step-by-step answer:
M and N are two sets.

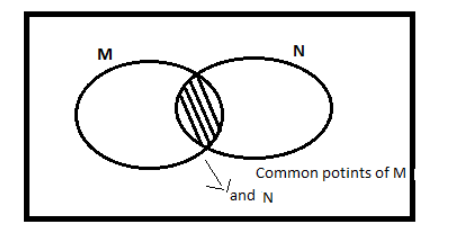
So, probability of getting M as a result is = P ( M )
And probability of getting N = P ( N )
And the probability of getting both i.e. ( P ( M ) and P ( N ) = \[P(M \cap N)\]
As we know that only 1 event can occur at time.
So, probability of getting exactly one occur
\[ \Rightarrow \] P ( Getting only a event ) = P ( M ) + P( N ) – P ( M \[ \cap \] N ) (whether it is event M or N)
This is because we want only a event and P ( M ) and P ( N ) are the events which are exactly one but P ( M \[ \cap \] N ) consists both the events together so we had subtract it from the exactly one events ( i.e. event M and N here ).ss
Now\[\]P ( Getting only a event ) = P ( M ) + P( N ) – P ( M \[ \cap \] N ) - P ( N \[ \cap \] M )
\[ \Rightarrow \] P ( M ) + P ( N ) – 2P ( M \[ \cap \]N ) ( as P ( M \[ \cap \] N ) = P ( N \[ \cap \] M ) )
Hence the correct option is A.


Note:Whenever we find difficulty in solving such types of problems it is very easy to draw the Venn’s diagram with the help of data given in question. The Venn diagram will solve this problem quickly. Here the two sets are equal so the common points or we can say the intersection points of such questions are always the same and equal to each other. And with all this knowledge we will find the result quickly and accurately.