Question

If $\left( x,y \right)$ are any point on the parabola ${{y}^{2}}=4x$ . Let $P$ be the point that divides the line segment from $\left( 0,0 \right)$ to $\left( x,y \right)$ in the ratio $1:3$. Then, the locus of $P$ is:
(1) ${{x}^{2}}=y$
(2) ${{y}^{2}}=2xy$
(3) ${{y}^{2}}=x$
(4) ${{x}^{2}}=2y$

Answer 1

Hint:Here in this question we have been asked to find the locus of $P$ given that $\left( x,y \right)$ is any point on the parabola ${{y}^{2}}=4x$ and $P$ be the point that divides the line segment from $\left( 0,0 \right)$ to $\left( x,y \right)$ in the ratio $1:3$ . To answer this question we will assume the coordinates of $P$ to be $\left( h,k \right)$ and find the condition in which it can divide the line segment.

Complete step-by-step solution:
Now considering from the question we have been asked to find the locus of $P$ given that $\left( x,y \right)$ is any point on the parabola ${{y}^{2}}=4x$ and $P$ be the point that divides the line segment from $\left( 0,0 \right)$ to $\left( x,y \right)$ in the ratio $1:3$ .

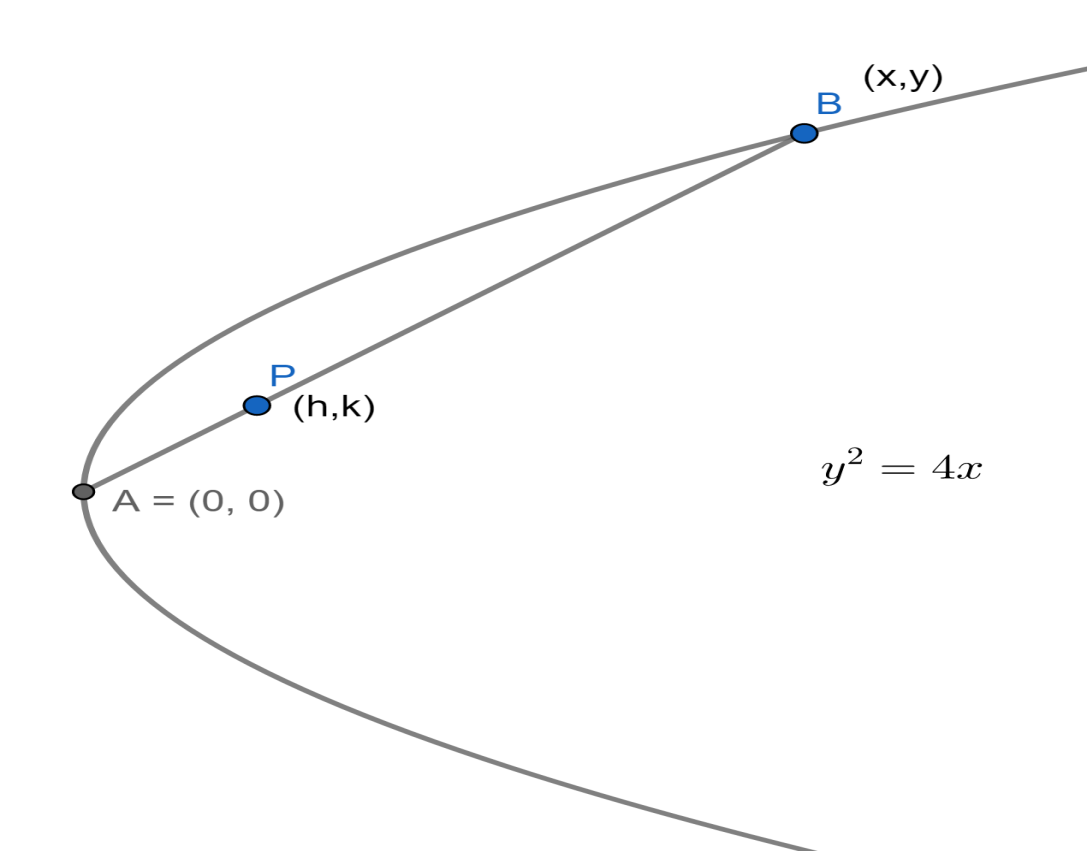
From the basic concepts of straight lines, we know that the section formula states that when any point divides the line segment formed by $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio of $m:n$ internally then it is given as $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ .
Let us assume that the coordinates of $P$ are $\left( h,k \right)$.
Now we will use the statement “ $P$ divides the line segment from $\left( 0,0 \right)$ to $\left( x,y \right)$ in the ratio$1:3$” and conclude that $h=\dfrac{1\left( x \right)+3\left( 0 \right)}{1+3}$ and $k=\dfrac{1\left( y \right)+3\left( 0 \right)}{1+3}$ .
Hence $h=\dfrac{x}{4}$ and $k=\dfrac{y}{4}$ .
Since it is given that $\left( x,y \right)$ is located on the parabola ${{y}^{2}}=4x$ we will get
$\begin{align}
  & {{\left( 4k \right)}^{2}}=4\left( 4h \right) \\
 & \Rightarrow {{k}^{2}}=h \\
\end{align}$ .
Therefore we can conclude that the locus of $P$ will be given as ${{y}^{2}}=x$ .
Hence we will mark the option “3” as correct.

Note:During the process of answering questions of this type we should be sure with the concepts that we are going to apply and calculations that we are going to perform between the steps. If someone had a misconception that the section formula is given as $\left( \dfrac{m{{x}_{1}}+n{{x}_{2}}}{m+n},\dfrac{m{{y}_{1}}+n{{y}_{2}}}{m+n} \right)$ then they will end up having the conclusion as ${{y}^{2}}=3x$ which is not present in the options and a wrong answer.