Question

If \[\left( {{\alpha }^{2}},\alpha -2 \right)\] be a point interior to the region of the parabola \[{{y}^{2}}=2x\] bounded by the chord joining the points (2, 2) and (8, -4) then P belongs to the interval
(a)\[-2+2\sqrt{2}<\alpha <2\]
(b)\[\alpha >-2+2\sqrt{2}\]
(c)\[\alpha >-2-2\sqrt{2}\]
(d)None of these

Answer 1

Hint: Any point \[\left( {{x}_{1}},{{y}_{1}} \right)\] lying inside of any conic S = 0 will satisfy the equation, \[S\left( {{x}_{1}},{{y}_{1}} \right)<0\], where S is the standard form of conic. Put (0, 0) to the chord and determine the sign of it and hence, according to it the sign will change, while putting \[\left( {{\alpha }^{2}},\alpha -2 \right)\] to the equation of chord. If they point to chords and use ‘< 0’ and vice – versa for positive sign (> 0). Solve the two inequalities calculated with the help of two conditions mentioned above. Take their intersection to get the answer.

Complete step-by-step answer:
Here, we have to find the interval for \[\alpha \], if it is given that \[\left( {{\alpha }^{2}},\alpha -2 \right)\] is a point lying in the region of the parabola \[{{y}^{2}}=4x\] bounded by the chord joining the points (2, 2) and (8, -4).
So, diagram with the help of the given informations can be given as,

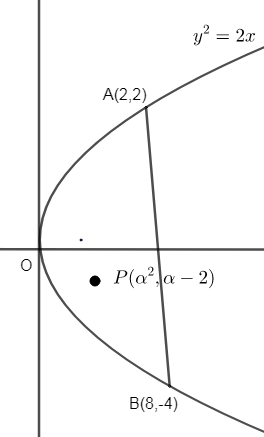
Let us find out the equation of the line passing through the points A and B.
We know equation of a line with given two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] as,
\[y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)-(i)\]
Now, we have two points A and B, so, we can get the equation of line passing through A and B as,
\[\begin{align}
  & y-2=\dfrac{-4-2}{8-2}\left( x-2 \right) \\
 & y-2=\dfrac{-6}{6}\left( x-2 \right) \\
 & y-2=-1\left( x-2 \right) \\
 & y-2=-x+2 \\
 & x+y=4 \\
\end{align}\]
Or
\[x+y-4=0-(ii)\]
Now, as \[\left( {{\alpha }^{2}},\alpha -2 \right)\] is lying inside the region of parabola. And we know if any point lies inside the curve, S = 0, then
\[S\left( {{x}_{1}},{{y}_{1}} \right)<0-(iii)\]
Where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is a point lying inside the curve S.
So, as equation of parabola given is,
\[{{y}^{2}}-2x=0-(iv)\]
Now, as \[\left( {{\alpha }^{2}},\alpha -2 \right)\] is lying inside the curve (iv). So, using equation (iii), we get,
\[\begin{align}
  & {{\left( \alpha -2 \right)}^{2}}-2{{\alpha }^{2}}<0 \\
 & {{\alpha }^{2}}+4-4\alpha -2{{\alpha }^{2}}<0 \\
 & -{{\alpha }^{2}}-4\alpha +4<0 \\
\end{align}\]
Multiplying with -1 will change the above inequality. So, we get,
\[{{\alpha }^{2}}+4\alpha -4>0-(v)\]
Now, we can find roots of equation \[{{\alpha }^{2}}+4\alpha -4=0\] by using the quadratic formula given for any quadratic \[a{{x}^{2}}+bx+c=0\] as,
\[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}-(vi)\]
Hence, roots of equation (v), we get,
\[\begin{align}
  & =\dfrac{-4\pm \sqrt{16-4\times \left( -4 \right)}}{2\times 1} \\
 & =\dfrac{-4\pm \sqrt{16+16}}{2} \\
 & =\dfrac{-4\pm \sqrt{32}}{2}=\dfrac{-4\pm 4 \sqrt{2}}{2} \\
 & =-2\pm 2\sqrt{2} \\
\end{align}\]
Now, we can write the equation (v) as,
\[\left( \alpha -\left( -2+2\sqrt{2} \right) \right)\left( \alpha +\left( -2-2\sqrt{2} \right) \right)>0\]
We know,
If \[\left( x-a \right)\left( x-b \right)>0\]
Then, \[x\in \left( -\infty ,a \right)\cup \left( b,\infty \right)\], where (a < b).
So, we get,
\[\begin{align}
  & \left( \alpha -\left( -2+2\sqrt{2} \right) \right)\left( \alpha -\left( -2-2\sqrt{2} \right) \right)>0 \\
 & \alpha \in \left( -\infty ,-2-2\sqrt{2} \right)\cup \left( -2+2\sqrt{2},\infty \right)-(vii) \\
\end{align}\]
Now, as the point \[\left( {{\alpha }^{2}},\alpha -2 \right)\] is lying left to the equation represented by line segment AB. i.e. \[x+y-4=0\].
Now, as we can observe (0, 0) is also lying on the left hand side of the line, so the sign given by putting (0, 0) to (x + y -4) is same as sign by putting \[\left( {{\alpha }^{2}},\alpha -2 \right)\] to \[x+y-4=0\].
So, putting (0, 0) to the line \[x+y-4=0\], we get,
\[0+0-4=-4<0\]
Hence, \[\left( {{\alpha }^{2}},\alpha -2 \right)\] will also give less than 0 by putting it to \[x+y-4=0\].
So, we get,
\[\begin{align}
  & {{\alpha }^{2}}+\alpha -2-4<0 \\
 & {{\alpha }^{2}}+\alpha -6<0 \\
\end{align}\]
We can factorize the equation as,
\[\begin{align}
  & {{\alpha }^{2}}+3\alpha -2\alpha -6<0 \\
 & \alpha \left( \alpha +3 \right)-2\left( \alpha +3 \right)<0 \\
 & \left( \alpha -2 \right)\left( \alpha +3 \right)<0 \\
\end{align}\]
We know,
If \[\left( x-a \right)\left( x-b \right)<0\]
\[x\in \left( a,b \right)\], where a < b
Hence, we get,
\[\begin{align}
  & \left( \alpha -2 \right)\left( \alpha +3 \right)<0 \\
 & \left( \alpha -2 \right)\left( \alpha -\left( -3 \right) \right)<0 \\
 & \alpha \in \left( -3,2 \right)-(viii) \\
\end{align}\]
Now, we know the range of \[\alpha \] with respect to parabola as well as with respect to line AB as well. But we need to find ‘\[\alpha \]’, where both conditions are satisfied. So, we need to take the intersection of the ranges of \[\alpha \] from equations (vii) and (viii).

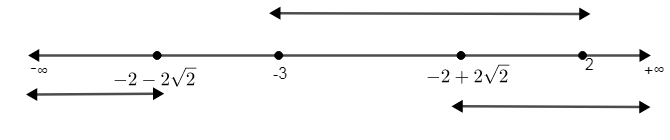
Now, we can observe from the above representation of intervals, we get the intersection of \[\alpha \] as,
\[\alpha \in \left( -2+2\sqrt{2},2 \right)\]
Or
\[-2+2\sqrt{2}<\alpha <2\]
Hence, option (a) is the correct answer.

Note: One may go wrong if he / she put \[\left( {{\alpha }^{2}},\alpha -2 \right)\] to the equation \[2x-{{y}^{2}}=0\] and put the same inequality i.e. ‘<’. Here, we need to use only standard form of curves i.e. \[{{y}^{2}}-4ax=0\] or \[ax+by+c=0\], not any other form, otherwise, we need to change the inequality as well according to the equation.
One may use a number line for the inequalities \[\left( x-a \right)\left( x-b \right)<0\] or \[\left( x-a \right)\left( x-b \right)>0\] as well. We used the direct results of these inequalities in the solution. So, try to remember the results for future reference with these kinds of questions.