Question

If $\left( {a,{a^2}} \right)$ falls inside the angle made by the lines $y = \dfrac{x}{2}$, $x > 0$ and $y = 3x$, $x > 0$, then $a$ belong to
(a) $\left( {0,\dfrac{1}{2}} \right)$
(b) \[\left( {3,\infty } \right)\]
(c) $\left( {\dfrac{1}{2},3} \right)$
(d) $\left( { - 3, - \dfrac{1}{2}} \right)$

Answer 1

Hint:
We will first draw the lines $y = \dfrac{x}{2}$ and $y = 3x$. Now the point $\left( {a,{a^2}} \right)$ must lie between the lines. Hence, the value of $a$ must satisfy the inequalities ${a^2} - \dfrac{a}{2} > 0$ and ${a^2} - 3a < 0$. Plot the roots on the number line and find the intersection of the values that satisfy the value of $a$.

Complete step by step solution:
We are given that there are two lines, $y = \dfrac{x}{2}$ and $y = 3x$.
Let us first draw these lines on the graph.

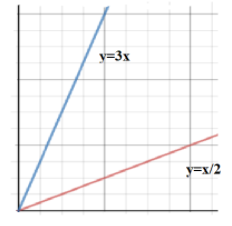
We have to find the values for which the point $\left( {a,{a^2}} \right)$ should lie between the lines $y = \dfrac{x}{2}$ and $y = 3x$.
If we substitute $a$ for $x$ and ${a^2}$ for $y$
Then, ${a^2} - \dfrac{a}{2} > 0$ and ${a^2} - 3a < 0$ for the point to lie between the lines.
We have to solve both the inequalities.
If ${a^2} - \dfrac{a}{2} > 0$, this implies, $a\left( {a - \dfrac{1}{2}} \right) > 0$
Plot the roots on a number line.

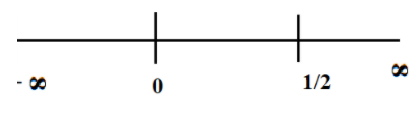
Take the testing point between $\dfrac{1}{2}$ and $\infty $, say 1
Then, $1\left( {1 - \dfrac{1}{2}} \right) > 0$ is true, then it is positive.
In the similar manner, we have,

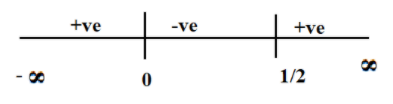
Hence, the required region here is $\left( { - \infty ,0} \right) \cup \left( {\dfrac{1}{2},\infty } \right)$
Next, find the region of ${a^2} - 3a < 0$ which is $a\left( {a - 3} \right) < 0$
Plot the roots and determine the sign.
Let 4 be the point between 3 and $\infty $, say 4.
$4\left( {4 - 3} \right) > 0$

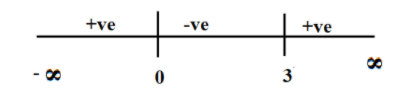
And the required area is $\left( {0,3} \right)$
We have to take the intersection of both the intervals.
$\left( {\left( { - \infty ,0} \right) \cup \left( {\dfrac{1}{2},\infty } \right)} \right) \cap \left( {0,3} \right) = \left( {\dfrac{1}{2},3} \right)$
Thus, $a$ belongs to $\left( {\dfrac{1}{2}, 3} \right)$

Hence, option (c) is correct.

Note:
Formation of the inequalities should be correct. Also, one must know how to find values of a given inequality. At last, do not forget to take intersection of the values of both the inequalities.