Question

If $\left( -1,2 \right),\left( 4,1 \right),\left( 7,16 \right)$ are three vertices of a parallelogram taken in order, then the fourth vertex and also the areas of the parallelogram are
A. $\left( -4,3 \right),16sq.unit$
B. $\left( 2,17 \right),78sq.unit$
C. $\left( -8,3 \right),24sq.unit$
D. $\left( 10,-5 \right),36sq.unit$

Answer 1

Hint: We will start by using the fact that the diagonals of a parallelogram bisect each other. Then we will let the fourth vertex be $\left( {{x}_{1}},{{y}_{1}} \right)$ and apply the midpoint formula to find the midpoint of both the opposite pair of vertices and equate them to find the fourth vertex. Then we will find the area of two sub triangle by using coordinate formula determinant $A=\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\
   {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\
   1 & 1 & 1 \\
\end{matrix} \right|$.

Complete step-by-step answer:
Now, we have been given that the three vertices of a parallelogram are $\left( -1,2 \right),\left( 4,1 \right),\left( 7,16 \right)$.

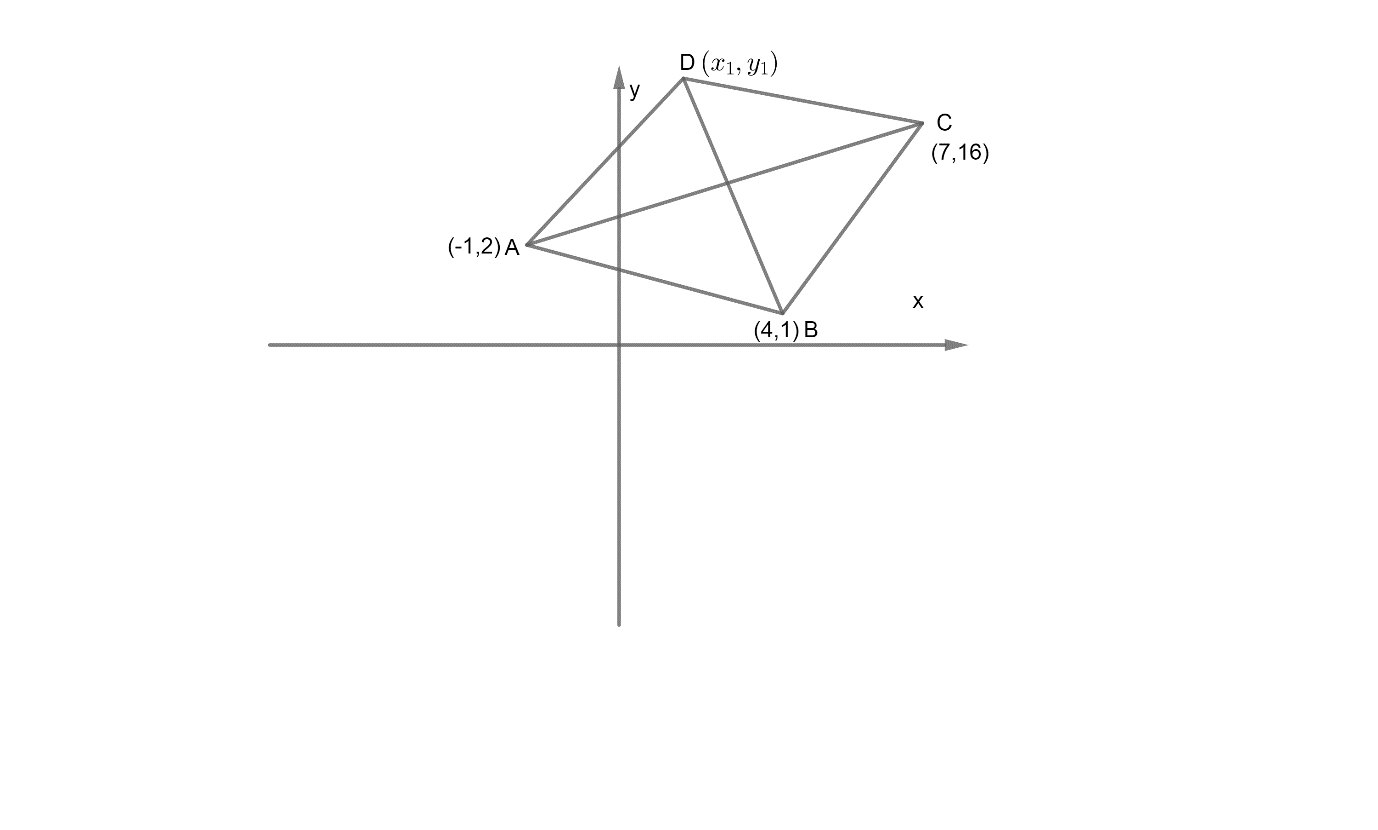
Now, we let the fourth vertex be $\left( {{x}_{1}},{{y}_{1}} \right)$.
Now, we know that the midpoint of vertex $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Since, we know that the diagonals of a parallelogram bisect each other. Therefore, we have,
$\left( \dfrac{-1+7}{2},\dfrac{16+2}{2} \right)=\left( \dfrac{{{x}_{1}}+4}{2},\dfrac{{{y}_{1}}+1}{2} \right)$
On comparing both coordinates we have,
$\begin{align}
  & \dfrac{6}{2}=\dfrac{{{x}_{1}}+4}{2} \\
 & 6-4={{x}_{1}} \\
 & 2={{x}_{1}} \\
 & \dfrac{16+2}{2}=\dfrac{{{y}_{1}}+1}{2} \\
 & 18-1={{y}_{1}} \\
 & 17={{y}_{1}} \\
\end{align}$
Hence, the fourth vertex is $\left( 2,17 \right)$.
Now, we know that the diagonal of a parallelogram divides it into two equal parts. So, we have area of triangle in coordinate system as,
$A=\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\
   {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\
   1 & 1 & 1 \\
\end{matrix} \right|$
So, we have area of \[\Delta ACB=\]$\dfrac{1}{2}\left| \begin{matrix}
   -1 & 4 & 7 \\
   2 & 1 & 16 \\
   1 & 1 & 1 \\
\end{matrix} \right|$
Now, expanding along ${{R}_{3}}$ we have,
$\begin{align}
  &= \dfrac{1}{2}\left\{ 1\left( 64-7 \right)-1\left( -16-14 \right)+1\left( -1-8 \right) \right\} \\
 & =\dfrac{1}{2}\left\{ 57-1\left( -30 \right)+1\left( -9 \right) \right\} \\
 &= \dfrac{1}{2}\left\{ 57+30-9 \right\} \\
 &= \dfrac{1}{2}\left\{ 87-9 \right\} \\
 &= \dfrac{1}{2}\times 78 \\
\end{align}$
Now, we have the $ar\Delta ACB=ar\Delta DCA=\dfrac{78}{2}$.
Therefore, we have an area of parallelogram as 78 sq. units.
Hence, the correct option is (B).

Note: It is important to note that for finding the fourth vertex we have used the fact that at midpoint both pairs of opposite vertex will be the same. Also, it is important to note that for finding the area of triangle we have used the formula that $ar=\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\
   {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\
   1 & 1 & 1 \\
\end{matrix} \right|$. We must make sure not to make a mistake in sign of the terms while finding the area by expanding the determinant.