Question

If \[\left( {1{\text{ }},2} \right),\left( {4,y} \right),\left( {x,6} \right)\] and \[(3,5)\] are the vertices of a parallelogram taken in order , find x and y

Answer 1

Hint: Use the property that diagonals of a parallelogram bisect each other. Then use the concept of midpoint in the coordinates of the centre of both the diagonals and equate the coordinates for the required values.

Complete step-by-step answer:
Lets say A,B,C,D are the vertices of a parallelogram ABCD and O is the midpoint where diagonals AC and BD intersect each other.
\[A\left( {1,2} \right)\;B\left( {4,y} \right)\;C\left( {x,6} \right)\;D\left( {3,5} \right)\]

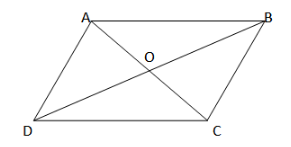
Now we have to find the coordinates of midpoint i.e. O
x- coordinate of O = $ \dfrac{{{x_1} + {x_2}}}{2} $
y- coordinate of O = $ \dfrac{{{y_1} + {y_2}}}{2} $
where $ x_1 $ = 1 and $ x_2 $ =x
 $ y_1 $ =2 and $ y_2 $ =6
we will put values to find the coordinates of point O
x – coordinate of O = $ y = 3 $ $ \dfrac{{1 + x}}{2} $
y – coordinate of O = $ \dfrac{{2 + 6}}{2} $ = $ \dfrac{8}{2} $ = 4
coordinates of point O =( $ \dfrac{{1 + X}}{2} $ , 4 ) ... ....(1)
We will repeat the same process but now we will consider diagonal BD and find the O coordinated by taking B and D coordinates into consideration.
x- coordinate of O = $ \dfrac{{{x_1} + {x_2}}}{2} $
y- coordinate of O = $ \dfrac{{{y_1} + {y_2}}}{2} $
where $ x_1 $ = 4 and $ x_2 $ =3
 $ y_1 $ =y and $ y_2 $ =5
we will put values to find the coordinates of point O
x – coordinate of O = $ \dfrac{{4 + 3}}{2} $ = $ \dfrac{7}{2} $
y – coordinate of O = $ \dfrac{{y + 5}}{2} $
coordinates of point O = $ (\dfrac{7}{2},\dfrac{{y + 5}}{2}) $ .....(2)
now we will compare equation 1 and 2
  $ (\dfrac{{1 + x}}{2},4) $ = $ (\dfrac{7}{2},\dfrac{{y + 5}}{2}) $
We will compare x and y coordinates and find the value of x and y
 $ \Rightarrow \dfrac{{1 + x}}{2} = \dfrac{7}{2} $
 $ \Rightarrow 1 + x = 7 $
 $ \Rightarrow x = 7 - 1 $
 $ \Rightarrow x = 6 $
Similarly we will find the value of y
 $ \Rightarrow 4 = \dfrac{{y + 5}}{2} $
 $ \Rightarrow 8 = y + 5 $
 $ \Rightarrow y = 8 - 5 $
 $ \Rightarrow y = 3 $
Therefore the $ x=6 $ and $ y=3 $ is the required answer.

Note: Revise the property of parallelogram that both the diagonals of parallelogram bisect each other. Revise the concept of midpoint of a line with the help of coordinates of endpoints of the line. Also mark the vertices ethier in clockwise direction or counterclockwise directions