
If l and m are intersecting lines, l $\parallel $ p and m $\parallel $ q, then which of the following statements is true?
A. l is parallel to q
B. m is parallel to p
C. p and q intersect
D. p is parallel to q
Answer
598.5k+ views
Hint: We will assume that p is parallel to q and try to show that our assumption is wrong, as parallel lines never intersect each other. The figure however will give a clear idea about the given data and the required result.
Complete step-by-step answer:
It is given in the question that l and m are intersecting lines. Then, we have to find the correct option from the options given in the question.
So, we know that p $\parallel $ l and q $\parallel $ m, it can be represented diagrammatically as given below:
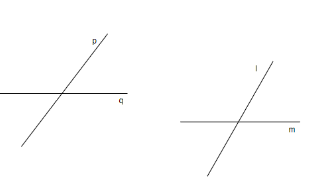
Let us assume that p and q do not intersect which means that p $\parallel $ q because parallel lines never intersect with each other. Hence, we get p $\parallel $ q. But we know that p $\parallel $ l and q $\parallel $ m, as it is given in the question.
We know that if there are three lines, a, b and c, and if a $\parallel $ b and also a $\parallel $ c, then we can understand that b $\parallel $ c. As we had assumed that p $\parallel $ q, and we know that p $\parallel $ l is given in the question, so we can write p $\parallel $ l as q $\parallel $ l. So, we will get q $\parallel $ l and q $\parallel $ m, which means that l $\parallel $ m. Hence, we get l $\parallel $ m. But we are given the question l intersects m, therefore our assumption is wrong. Hence, p intersects q.
Thus, option (C) is the correct answer.
Note: We can also solve this question by eliminating the options given in the question. It is given that l $\parallel $ p and m $\parallel $ q and also it is said that lines l and m intersect. So, now the options, l is parallel to q and m is parallel to p cannot be possible. Since l and m intersect, it is clear that p and q will also intersect. But, there is a chance of going wrong using this method as it is difficult to visualise. So, it is advised to always draw a rough figure first and then come to a conclusion.
Complete step-by-step answer:
It is given in the question that l and m are intersecting lines. Then, we have to find the correct option from the options given in the question.
So, we know that p $\parallel $ l and q $\parallel $ m, it can be represented diagrammatically as given below:
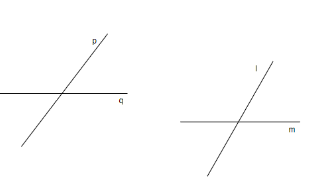
Let us assume that p and q do not intersect which means that p $\parallel $ q because parallel lines never intersect with each other. Hence, we get p $\parallel $ q. But we know that p $\parallel $ l and q $\parallel $ m, as it is given in the question.
We know that if there are three lines, a, b and c, and if a $\parallel $ b and also a $\parallel $ c, then we can understand that b $\parallel $ c. As we had assumed that p $\parallel $ q, and we know that p $\parallel $ l is given in the question, so we can write p $\parallel $ l as q $\parallel $ l. So, we will get q $\parallel $ l and q $\parallel $ m, which means that l $\parallel $ m. Hence, we get l $\parallel $ m. But we are given the question l intersects m, therefore our assumption is wrong. Hence, p intersects q.
Thus, option (C) is the correct answer.
Note: We can also solve this question by eliminating the options given in the question. It is given that l $\parallel $ p and m $\parallel $ q and also it is said that lines l and m intersect. So, now the options, l is parallel to q and m is parallel to p cannot be possible. Since l and m intersect, it is clear that p and q will also intersect. But, there is a chance of going wrong using this method as it is difficult to visualise. So, it is advised to always draw a rough figure first and then come to a conclusion.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




