Question

“If it is a good watch then it is a Titan watch. It is a Titan watch, therefore, it is a good watch “. This argument is :
A) Valid
B) Invalid
C) May be valid or invalid
D) Invalid if conditional connective is replaced by a biconditional connective.

Answer 1

Hint: We will use the Venn diagram to solve this problem and then do some logical reasoning to get the answer.
A Venn diagram is a diagram that shows all possible logical relations between a finite collection of different sets.

Complete step by step solution:
According to the first statement, it is given that:
If it is a good watch then it is a Titan watch. It means that all the good watches are titan watches.
Therefore if we draw the Venn diagram of the given statement we get:
Titan watches as the superset while the set of good watches as the inner set hence,:

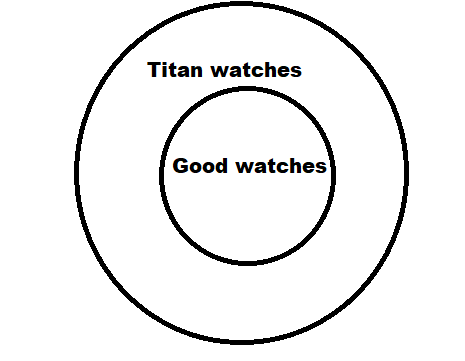
Now if we take an element in the superset of titan watches then it may not fall in the inner set of good watches which means not all titan watches are good watches.
Hence the second given statement:- “It is a Titan watch, therefore, it is a good watch” is not correct.

$\therefore$ Hence the given argument is invalid. So, Option B is correct.

Note:
Both the given statements should be considered separately one by one and also the Venn diagram drawn should be correct in order to get the right solution.