Question

If isosceles triangle PQR, \[PQ=PR=5cm\] is inscribed in a circle of radius 15cm. Find the area of the triangle.

Answer 1

Hint: First, we will draw the figure as per the given data in question. Then quadrilaterals will be formed in kite shape whose diagonals are perpendicular to each other. Figure will be like

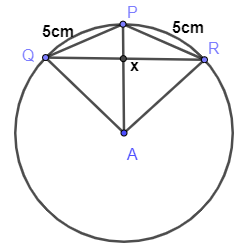
Then, we will assume the value of PX as x. We will find value of QX using Pythagoras theorem i.e. \[{{\left( side1 \right)}^{2}}+{{\left( side2 \right)}^{2}}={{\left( hypotenuse \right)}^{2}}\] . Then, we will find the value of AX using the \[AP=AX+PX\] . Then again, we will use Pythagoras theorem in triangle AXQ. On solving, we will get the value of x. By putting the value of x in the equation we will get the exact value of AP and QX. Then, we will use a formula to find the area of the triangle PQR given as \[area=\dfrac{1}{2}\times QR\times AX\] .

Complete step by step solution:
Here, we are given that length of triangle PQR i.e. \[PQ=PR=5cm\] and radius of circle is 15cm. So, figure will be as shown below.

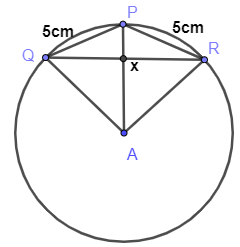
So, here radius will be \[AP=AQ=AR=15cm\] . Therefore, quadrilateral ARPQ will be kite. We know that diagonals of kite are perpendicular to each other i.e. \[AP\bot QR\] .
\[\therefore AX\bot QR\]
Now, we will assume let \[PX=x\text{ }cm\] .
Now, in right angles triangle PXQ, we will be using Pythagoras theorem i.e. \[{{\left( side1 \right)}^{2}}+{{\left( side2 \right)}^{2}}={{\left( hypotenuse \right)}^{2}}\] so, we will get as
\[{{\left( PX \right)}^{2}}+{{\left( QX \right)}^{2}}={{\left( PQ \right)}^{2}}\]
On substituting the values, we get
\[{{\left( x \right)}^{2}}+{{\left( QX \right)}^{2}}={{\left( 5 \right)}^{2}}\]
Now, on further solving and rearranging the terms, we get
\[Q{{X}^{2}}={{5}^{2}}-{{x}^{2}}=25-{{x}^{2}}\] …………………………………………(1)
Now, length of radius AP can be given to \[AP=AX+PX\] . So, on substituting the values, we get AX as
\[AX=AP-PX=15-x\] cm……………………………..(2)
Now, we will take the right angles triangle AXQ. Here, also using Pythagoras theorem we will get as
\[A{{X}^{2}}+Q{{X}^{2}}=A{{Q}^{2}}\]
We will substitute the values of equation (1) and (2), and radius of circle, we will get as
\[{{\left( 15-x \right)}^{2}}+25-{{x}^{2}}={{\left( 15 \right)}^{2}}\]
We will use the formula \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\] and on further solving, we will get as
\[225+{{x}^{2}}-30x+25-{{x}^{2}}=225\]
On cancelling the terms, we get
\[-30x=-25\]
\[x=\dfrac{-25}{-30}=\dfrac{5}{6}cm\] ……………………………………..(3)
On substituting this vale of x inequation (1) and on solving, we get
\[Q{{X}^{2}}=25-{{\left( \dfrac{5}{6} \right)}^{2}}=25-\dfrac{25}{36}\]
Now, we will take LCM and solving further we get
\[Q{{X}^{2}}=\dfrac{900-25}{36}=\dfrac{875}{36}\]
Now, taking square root on both the sides, we get
\[QX=\sqrt{\dfrac{875}{36}}=\dfrac{1}{6}\sqrt{875}cm\] …………………………..(4)
We will substitute value of equation (3) in equation (2), so we will get
\[AX=AP-PX=15-\dfrac{5}{6}=\dfrac{90-5}{6}=\dfrac{85}{6}cm\] ……………………………………..(5)
Also, we know that in \[\Delta PQR\] isosceles triangle, \[AX\bot QR\].
\[\therefore QX=RX\]
So, we can write as \[QR=2QX\] .
On substituting the value of QX from equation (4), we get
\[QR=2\times \dfrac{\sqrt{875}}{6}=\dfrac{2\sqrt{875}}{6}cm\] ………………………………….(6)
Thus, we can say that area of \[\Delta PQR\] can be find using the formula as
\[area=\dfrac{1}{2}\times base\times perpendicular\]
\[area=\dfrac{1}{2}\times QR\times AX=\dfrac{1}{2}\times \dfrac{2\sqrt{875}}{6}\times \dfrac{85}{6}\]
On solving, we get
\[area=\dfrac{85\sqrt{875}}{36}c{{m}^{2}}\]
Thus, area of triangle PQR is \[\dfrac{85\sqrt{875}}{36}c{{m}^{2}}\] or 69.842 \[c{{m}^{2}}\] .


Note: Be careful in this type of sum. Do not assume that in \[\Delta PQR\] , PQ and QR are of equal sides, so we can consider the third side as hypotenuse and can be found using Pythagoras theorem. Then the figure will be like this only

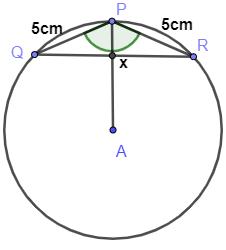
Here, angle P is not the right angle so Pythagoras theorem cannot be used here. So, do not make this mistake. Also, students should know that diagonals of quadrilateral bisect each other. Then only, the whole problem will be solved otherwise there are chances to get caught up in the middle of the problem and answers will be obtained. So, please be careful in this type of question.