Question

If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then prove that two triangles are congruent.

Answer 1

Hint:First of all draw the two right triangles for better visualization then as it is given that the hypotenuse and one side of the triangle is equal to hypotenuse and one side of the other triangle. We can prove the congruence of two triangles by SAS rule, as two sides of the triangles are already given equal and as the two triangles are right angled so the angle $ {{90}^{0}} $ is also the same.

Complete step-by-step answer:
In the below diagram, we have shown two right triangles ABC and DEF.
 

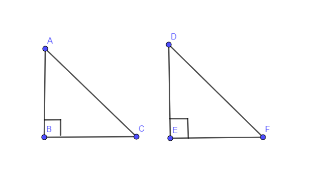
In the above two right triangles, it is given that the hypotenuse and one side of the triangle is equal to the hypotenuse and the other side of the triangle.
We have to prove that the above two triangles are congruent.
In $ \Delta ABC\And \Delta DEF $ ,
Hypotenuse is equal in both the two right triangles.
 $ AC=DF $
One side of the triangle is equal to the other side of the triangle. Let us assume that the two sides are equal.
 $ AB=DE $
 The two triangles are right angled so both the triangles have $ {{90}^{0}} $ in common.
 $ \angle ABC=\angle DEF $
From the above, the two triangles ABC and DEF are congruent by SAS rule.
In SAS rule, the two triangles have two sides along with one angle are equal.
Hence, we have proved the two triangles as congruent.

Note: Instead of taking AB and DE as equal we can also take BC and EF as equal because it is given that one side of the one triangle is equal to the one side of the other triangle, it has not mentioned specifically that which side is equal so we have the freedom to choose equal sides in the two triangles.
One more thing whichever sides you choose apart from the hypotenuse, the SAS rule will be satisfied because this rule contains two sides should be equal along with one angle.