Question

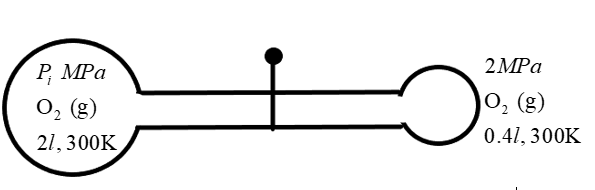
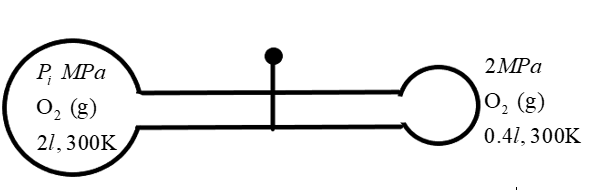
If in the below diagram after opening the valve, final pressure is \[\dfrac{7}{6}MPa\], then find the initial pressure \[{{P}_{1}}\text{ }(in\text{ }MPa)\].

Answer 1

Hint: We are given two containers connected by a pipe which has unequal pressure and volume conditions initially. The thermodynamic variables are kept steady by separating them with a valve, which is opened later. We can use the gas law to solve the unknown variable.

Complete step by step answer:
We are given a condition in which unequal states of thermodynamic conditions mix with each other resulting in another state. Two bulb-like containers of volume \[{{\text{V}}_{1\,}}\text{ and }{{\text{V}}_{2}}\] contains gaseous oxygen at pressure \[{{P}_{1}}\text{ and }{{P}_{2}}\]respectively at a temperature 300K. We know that the gaseous oxygen tends to have a different number of molecules at different thermodynamic conditions. So, initially the number of molecules in the containers are given as \[{{n}_{1}}\text{ and }{{\text{n}}_{2}}\] respectively.
  

Now, let us consider the situation when the valve is opened. We know for sure that the oxygen molecules tend to move across the pipe due to the pressure difference at the two ends. So, what we have to calculate is the resulting conditions which will be observed as a result of this opening.
For this, we can apply the gas law. The gas law is given as –
\[PV=nRT\]
Where, P is the pressure in the container,
V is the volume of the container,
n is the number of molecules in the container,
R is the gas constant, and,
T is the temperature in absolute scale.
Let us consider this gas law equation for the two containers in the initial condition.
For first container,
\[\begin{align}
  & {{P}_{1}}{{V}_{1}}={{n}_{1}}RT \\
 & \therefore\ {{n}_{1}}=\dfrac{{{P}_{1}}{{V}_{1}}}{RT}\text{ -(1)} \\
\end{align}\]
For the second container,
\[\begin{align}
  & {{P}_{2}}{{V}_{2}}={{n}_{2}}RT \\
 & \therefore\ {{n}_{2}}=\dfrac{{{P}_{2}}{{V}_{2}}}{RT}\text{ --(2)} \\
\end{align}\]
From, (1) and (2), we get the number of molecules present in each container initially.
Now, let us consider the final condition where the valve is opened. In this case, we have to remember that the total number of molecules in the system remains constant, i.e., n is the sum of the number of molecules in both containers.
Applying the gas law to the final condition,
\[\begin{align}
  & {{P}_{f}}{{V}_{f}}=nRT \\
 & \therefore \ n=\dfrac{{{P}_{f}}{{V}_{f}}}{RT} \\
\end{align}\]
Now,
\[\begin{align}
  & n={{n}_{1}}+{{n}_{2}} \\
 & \Rightarrow \text{ }\dfrac{{{P}_{f}}{{V}_{f}}}{RT}=\dfrac{{{P}_{1}}{{V}_{1}}}{RT}+\dfrac{{{P}_{2}}{{V}_{2}}}{RT} \\
\end{align}\]
We can find the required pressure which is \[{{P}_{1}}\] by substituting given values in the above equation as –
\[\begin{align}
  & {{P}_{f}}=\dfrac{7}{6}MPa \\
 & {{P}_{2}}=2MPa \\
 & {{V}_{1}}=2l \\
 & {{V}_{2}}=0.4l \\
 & {{V}_{f}}=2.4l \\
 & \\
\end{align}\]
\[\begin{align}
  & {{P}_{f}}{{V}_{f}}={{P}_{1}}{{V}_{1}}+{{P}_{2}}{{V}_{2}} \\
 & \Rightarrow \text{ }\dfrac{7}{6}(2.4)={{P}_{1}}(2)+2(0.4) \\
 & \Rightarrow \text{ }2.8=2{{P}_{1}}+0.8 \\
 & \Rightarrow \text{ }{{P}_{1}}=\dfrac{2.8-0.8}{2} \\
 & \therefore\text{ }{{P}_{1}}=1MPa \\
\end{align}\]
The required pressure condition is 1 MPa initially in the first container.

Note:
We use the ideal gas condition for solving the thermodynamic variables when the temperature and pressure conditions are moderate. Most of the gases in normal temperatures and pressure conditions do not deviate much from the ideal gas conditions.