Question

If \[{{I}_{n}}\] is the area of n sided regular polygon inscribed in a circle of unit radius and \[{{O}_{n}}\] be the area of the polygon circumscribing the given circle, prove that,
\[{{I}_{n}}=\dfrac{{{O}_{n}}}{2}\left( 1+\sqrt{1-{{\left( \dfrac{2{{I}_{n}}}{n} \right)}^{2}}} \right)\]

Answer 1

Hint: To solve this question given above, first we will find the values of \[{{I}_{n}}\text{ and }{{O}_{n}}\] in terms of n only. For finding the values of \[{{I}_{n}}\text{ and }{{O}_{n}},\] we will divide the polygon into n triangles and then we will find the area of one triangle and then we will multiply it with n to obtain the total area.

Complete step-by-step answer:
To start with, we will find out the value of \[{{I}_{n}}.\] In the question, it is given that \[{{I}_{n}}\] is the area of n sided regular polygon inscribed in a circle of unit radius. Thus, first, we will draw a circle of radius 1m and then we will inscribe a polygon inside it as shown.

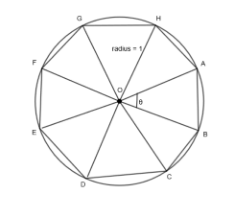
In the above figure, the n sided polygon is divided into n triangles by joining the center with the vertices of the polygon. Now, the total area of the polygon will be equal to the sum of the area of the individual triangles. The areas of all the triangles will be the same because each triangle is an isosceles triangle (two sides are radii) and the third side is the side of the regular polygon. So, we can say that the area of the polygon will be n times the area of the triangle BOC. Thus, we have,
\[\text{Area of the polygon}=n\times \left( \text{Area of }\Delta BOC \right)\]
\[\Rightarrow {{I}_{n}}=n\left( \text{Area of }\Delta BOC \right).....\left( i \right)\]
Now, the area of a triangle with two sides and an angle between them is given by:

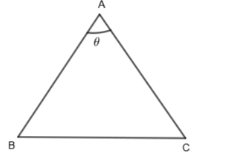
\[\text{Area of }\Delta ABC=\dfrac{1}{2}\times AB\times AC\times \sin \theta \]
Thus, we will have,
\[\Rightarrow {{I}_{n}}=n\left( \dfrac{1}{2}\times OB\times OC\times \sin \theta \right)\]
\[\Rightarrow {{I}_{n}}=n\times \dfrac{1}{2}\times 1\times 1\times \sin \theta \]
\[\Rightarrow {{I}_{n}}=\dfrac{n\sin \theta }{2}....\left( ii \right)\]
Now, we will calculate the value of \[\theta .\] The total angle inside the circle is \[2\pi .\] Now the circle is divided into n triangles, so,
\[\theta =\dfrac{2\pi }{n}....\left( iii \right)\]
Now, we will find out the value of \[{{O}_{n}}.\text{ }{{O}_{n}}\] is the area of the polygon circumscribing the circle of radius 1m. Thus, we have,

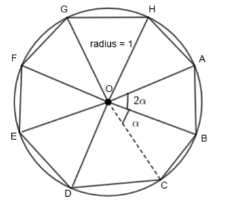
Now, we have drawn an n sided polygon circumscribing a circle and we have joined the center with the points on the edges which are touching the circle. The lines which join the center and these points will be normal to the circle because the sides of the polygon will be tangent to the given circle. Now, there are n similar quadrilaterals formed due to the joining by lines. So, we have,
\[\text{Area of the polygon}=n\times \left( \text{Area of quadrilateral }OCDE \right)....\left( iv \right)\]
Now, we will divide the quadrilateral into two triangles by the line OD. The area of the triangle OCD will be equal to triangle OED because the polygon is regular. Thus, we have,
\[\text{Area of quadrilateral }OCDE=2\times \text{ Area of }\Delta OCD\]
\[\text{Area of quadrilateral }OCDE=2\times \left( \dfrac{1}{2}\times OC\times OF\times \sin \alpha \right).....\left( v \right)\]
Now, we will consider the triangle OCD.

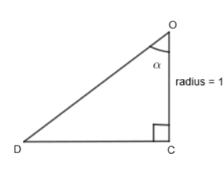
Now,
\[\dfrac{OC}{CD}=\cos \alpha \]
\[\Rightarrow \dfrac{1}{OD}=\cos \alpha \]
\[\Rightarrow OD=\dfrac{1}{\cos \alpha }\]
Also, there are n quadrilaterals, so the value of \[2\alpha \] will be \[\dfrac{2\pi }{n},\] so the value of \[\alpha =\dfrac{\pi }{n}.....\left( vi \right)\]
Putting the value of OC and OD in equation (v), we will get,
\[\text{Area of quadrilateral}=2\times \dfrac{1}{2}\times 1\times \dfrac{1}{\cos \alpha }\times \sin \alpha \]
\[\text{Area of quadrilateral}=\tan \alpha .....\left( vii \right)\]
From (iv) and (vii), we have,
\[\text{Area of polygon}=n\times \tan \alpha \]
\[\Rightarrow {{O}_{n}}=n\tan \alpha ....\left( viii \right)\]
Now, we will divide the equation (ii) by (viii). Thus, we get,
\[\dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{\dfrac{n\sin \theta }{2}}{n\tan \alpha }\]
\[\dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{\sin \theta }{2\tan \alpha }....\left( ix \right)\]
Now, we will put the values of \[\alpha \text{ and }\theta \] in (vi) and (iii) to (ix), we will get,
\[\dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{\sin \left( \dfrac{2\pi }{n} \right)}{2\tan \left( \dfrac{\pi }{n} \right)}\]
Now, we will use the following trigonometric identities
\[\tan x=\dfrac{\sin x}{\cos x}\]
\[\sin 2x=2\sin x\cos x\]
Thus, we have,
\[\dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{2\sin \left( \dfrac{\pi }{n} \right)\cos \left( \dfrac{\pi }{n} \right)}{2\left( \dfrac{\sin \left( \dfrac{\pi }{n} \right)}{\cos \left( \dfrac{\pi }{n} \right)} \right)}\]
\[\Rightarrow \dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{2{{\cos }^{2}}\left( \dfrac{\pi }{n} \right)}{2}\]
Now, we will use another trigonometric identity,
\[\cos 2\theta =2{{\cos }^{2}}\theta -1\]
\[\Rightarrow 2{{\cos }^{2}}\theta =1+\cos 2\theta \]
Thus, we will get,
\[\Rightarrow \dfrac{{{I}_{n}}}{{{O}_{n}}}=\dfrac{1+\cos \dfrac{2\pi }{n}}{2}\]
\[\Rightarrow \dfrac{2{{I}_{n}}}{{{O}_{n}}}=1+\cos \dfrac{2\pi }{n}\]
\[\Rightarrow {{I}_{n}}=\dfrac{{{O}_{n}}}{2}\left( 1+\cos \dfrac{2\pi }{n} \right)\]
Now, we will use the identity, \[\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }.\] Thus, we get,
\[\Rightarrow {{I}_{n}}=\dfrac{{{O}_{n}}}{2}\left[ 1+\sqrt{1-{{\sin }^{2}}\left( \dfrac{2\pi }{n} \right)} \right].....\left( x \right)\]
Now, we know that,
\[{{I}_{n}}=\dfrac{n}{2}\sin \theta =\dfrac{n}{2}\sin \left( \dfrac{2\pi }{n} \right)\]
\[\Rightarrow \sin \dfrac{2\pi }{n}=\dfrac{2{{I}_{n}}}{n}\]
\[\Rightarrow {{\sin }^{2}}\left( \dfrac{2\pi }{n} \right)={{\left( \dfrac{2{{I}_{n}}}{n} \right)}^{2}}....\left( xi \right)\]
From (x) and (xi), we have,
\[\Rightarrow {{I}_{n}}=\dfrac{{{O}_{n}}}{2}\left[ 1+\sqrt{1-{{\left( \dfrac{2{{I}_{n}}}{n} \right)}^{2}}} \right]\]
Hence proved.

Note: When we put n = 1 and n = 2 in the values of \[{{I}_{n}}\text{ and }{{O}_{n}}\] we will get 0, i.e, the area of the polygon will be zero in both the cases. It is true because when n = 1 and n = 2, we will not get any polygon, we will only get a line and so the area is zero.