Question

If in an ellipse, a focus is $\left( 6,7 \right)$, the corresponding directrix is $x+y+2=0$ and the eccentricity $=\dfrac{1}{2}$ , then the equation of the ellipse is :
(A). $7{{x}^{2}}+2xy+7{{y}^{2}}-44x-108y+684=0$
(B). $7{{x}^{2}}-2xy+7{{y}^{2}}-100x-116y+676=0$
(C). $9{{x}^{2}}-2xy+9{{y}^{2}}-44x-108y+684=0$
(D). None of these.

Answer 1

Hint: General equation of any conic is given by the relation $\dfrac{PS}{PM}=e$
Where P is any point on conics, S is one of the foci, and PM is the perpendicular distance of point P from the directrix, and e is the eccentricity of conic. So, put point P as $\left( x,y \right)$ and proceed further to get the equation of ellipse, use the following results:-
Distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Perpendicular distance of any point $\left( {{x}_{1}},{{y}_{1}} \right)$ from the line $ax+by+c=0$ is given as:
$=\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$
As we know the general equation of any conic is given by the formula
$\dfrac{PS}{PM}=e$………………………….. (1)
Where P is a point on the given conic and S is the focus of the conic and PM is a perpendicular distance of directrix from point P i.e. PM is perpendicular to the directrix of the conic and e is the eccentricity of conic.
Now, as we know distance between any two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is given by distance formula as: $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$……………………………….. (2)
And the perpendicular distance of any line $Ax+By+C=0$ from a general point $\left( {{x}_{1}},{{y}_{1}} \right)$is given as:
$=\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$……………………….. (3)
Now, coming to the question, we are given the focus of ellipse as $\left( 6,7 \right)$ , directrix as $x+y+2=0$ and eccentricity of the ellipse as $e=\dfrac{1}{2}$ , and hence, we need to determine the equation of the ellipse with the help of given information.
So, we can use equation (1) to get the equation of ellipse. Diagram with the help of given information can be drawn as:

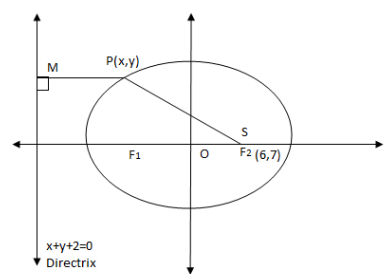
Where, P is a point taken on the ellipse, ${{F}_{1}}$ and ${{F}_{2}}$ are foci of the ellipse and $\left( 6,7 \right)$ i.e. the given focus in the problem is taken as S as well, M is the foot of perpendicular
Point from the directrix $x+y+2=0$ .
Now, we can get PS using distance formula, given in the equation (2) as:
$PS=\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}$ …………………………… (4)
And PM can be calculated with the help of equation (3) as PM is the perpendicular from the point P to the directrix.
So, we get PM as:
$PM=\left| \dfrac{x+y+2}{\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 1 \right)}^{2}}}} \right|=\left| \dfrac{x+y+2}{\sqrt{2}} \right|$
$PM=\left| \dfrac{x+y+2}{\sqrt{2}} \right|$ ………………………….. (5)
Now, we put values of PS and PM from the equation (4) and (5) and $e-\dfrac{1}{2}$ (given), in the equation (1) to get the equation of ellipse as:
$\dfrac{\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}}{\left| \dfrac{x+y+2}{\sqrt{2}} \right|}=\dfrac{1}{2}$
Now, on cross multiplying the above equation, we get –
$\left( \sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-7 \right)}^{2}}} \right)={{\left( \dfrac{1}{2}\times {\left| \dfrac{x+y+2}{\sqrt{2}} \right|} \right)}^{2}}$
${{\left( x-6 \right)}^{2}}+{{\left( y-7 \right)}^{2}}=\dfrac{1}{4}\times \dfrac{{\left(x+y+2\right)}^{2}}{{{\left( \sqrt{2} \right)}^{2}}}$……………………………….. (6)
Now, we know:
$\begin{align}
  & {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \\
 & {{\left( a+b+c \right)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ac \\
\end{align}$
So, we get the equation (6) using above two equations as:
$\begin{align}
  & {{x}^{2}}+36-12x+{{y}^{2}}+49-14y=\dfrac{1}{8}\left( {{x}^{2}}+{{y}^{2}}+4+2xy+4y+4x \right) \\
 & 8{{x}^{2}}+288-96x+8{{y}^{2}}+392-112y={{x}^{2}}+{{y}^{2}}+4+2xy+4y+4x \\
 & 8{{x}^{2}}-{{x}^{2}}+8{{y}^{2}}-{{y}^{2}}-96x-4x-112y-4y-2xy+288+392-4=0 \\
 & 7{{x}^{2}}+7{{y}^{2}}-100x-116y-2xy+676=0 \\
\end{align}$
Or
$7{{x}^{2}}-2xy+7{{y}^{2}}-100x-116y+676=0$
Hence, the equation of the ellipse is given by the above equation. So, option (B) is the correct answer.


Note: Another approach to get the equation of ellipse would be that we need to calculate the length of major and minor axis and equations of them as well with the help of given information in the problem and hence, apply the relation as:
$\dfrac{s_{1}^{2}}{{{a}^{2}}}+\dfrac{s_{2}^{2}}{{{b}^{2}}}-1$
Where ${{s}_{1}}$ and ${{s}_{2}}$ are equation of major and minor axis i.e. ${{s}_{1}}=0$ and ${{s}_{2}}=0$ and a and b are lengths of major and minor axis. Here, we need to apply concept as:
         (i) ${{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)$
        (ii) Directrix is perpendicular to the major axis and focus will lie on the major axis.
        (ii) Distance between focus and centre is equal to distance between focus and directrix.
But the above approach is much more complex than given in solution.
Mathematical calculation is also an important part of the solution and using the standard equation of any conic i.e. $\dfrac{PS}{PM}=e$ is the key point of the solution. So, remember this formula for future reference as well.