Question

If in a triangle, R and r are the circumradius and inradius respectively and ${{r}_{1}}$, ${{r}_{2}}$ and ${{r}_{3}}$ are in H.P. Find the H.M of the exradii of the triangle.
(a) $3r$
(b) $2R$
(c) $R+r$
(d) $\dfrac{1}{2R}$

Answer 1

Hint: We apply harmonic mean to ${{r}_{1}}$, ${{r}_{2}}$, ${{r}_{3}}$ and we substitute the formulas of them which are related to area and perimeter. After substitution and simultaneous calculation, we get a relation in a harmonic mean which gives us the final answer in terms of circumradius and inradius.

Complete step-by-step solution:
Let us assume that triangle ABC has a circumcircle of radius R, incircle of radius r, and excircles of radii ${{r}_{1}}$, ${{r}_{2}}$ and ${{r}_{3}}$. According to the problem, exradii ${{r}_{1}}$, ${{r}_{2}}$ and ${{r}_{3}}$ are in H.P (Harmonic Progression). We need to find the H.M (Harmonic Mean) of these exradii of the triangle.
We now draw the figure consisting of a triangle with all circumcircle, incircle, and all excircles.

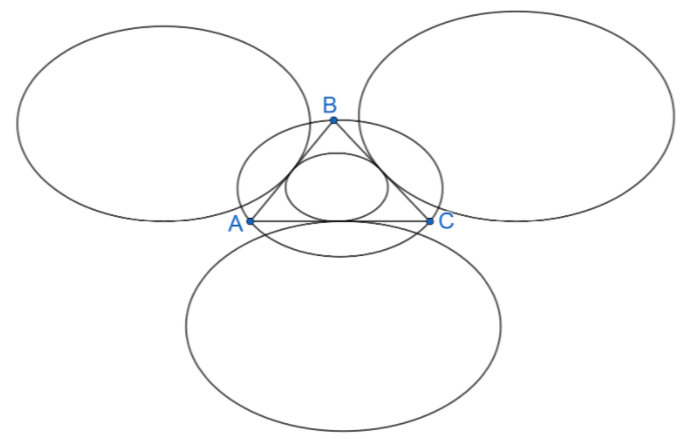
Let us assume the area of the triangle be A, sides opposite to vertices A, B and C are a, b and c. We assume the perimeter of the triangle be ‘2s’ and it is defined as $2s=a+b+c$.
We know that circumradius ‘R’ is defined as $R=\dfrac{abc}{4A}$, inradius ‘r’ is defined as $r=\dfrac{A}{s}$, exradii are defined as ${{r}_{1}}=\dfrac{A}{s-a}$, ${{r}_{2}}=\dfrac{A}{s-b}$, ${{r}_{3}}=\dfrac{A}{s-c}$.
It is given that we need to find H.M (Harmonic Mean) of ${{r}_{1}}$, ${{r}_{2}}$ and ${{r}_{3}}$.
We know that harmonic mean ‘n’ numbers ${{a}_{1}},{{a}_{2}},{{a}_{3}},......,{{a}_{n}}$ is $H.M=\dfrac{n}{\dfrac{1}{{{a}_{1}}}+\dfrac{1}{{{a}_{2}}}+\dfrac{1}{{{a}_{3}}}+......+\dfrac{1}{{{a}_{n}}}}$.
So, the H.M of ${{r}_{1}}$, ${{r}_{2}}$ and ${{r}_{3}}$ is $H.M=\dfrac{3}{\dfrac{1}{{{r}_{1}}}+\dfrac{1}{{{r}_{2}}}+\dfrac{1}{{{r}_{3}}}}$.
Now, we substitute ${{r}_{1}}=\dfrac{A}{s-a}$, ${{r}_{2}}=\dfrac{A}{s-b}$, ${{r}_{3}}=\dfrac{A}{s-c}$.
$H.M=\dfrac{3}{\dfrac{1}{\dfrac{A}{s-a}}+\dfrac{1}{\dfrac{A}{s-b}}+\dfrac{1}{\dfrac{A}{s-c}}}$.

$H.M=\dfrac{3}{\dfrac{s-a}{A}+\dfrac{s-b}{A}+\dfrac{s-c}{A}}$.
$H.M=\dfrac{3}{\dfrac{s-a+s-b+s-c}{A}}$.
$H.M=\dfrac{3A}{3s-(a+b+c)}$.
We know that perimeter $2s=a+b+c$ so, we substitute this in H.M.
\[H.M=\dfrac{3A}{3s-2s}\].
$H.M=\dfrac{3A}{s}$.
$H.M=3\times \left( \dfrac{A}{s} \right)$.
We know that inradius $r=\dfrac{A}{s}$.
$H.M=3r$.
∴ The Harmonic Mean (H.M) of exradii is 3r.
The correct option is (a).

Note: If we don’t remember the formulas, we need to derive the inradius, circumradius, and exradii of all the required circles which requires a heavy time. We should remember that the circumcircle passes through all the vertices of the triangle. Incircle has sides AB, BC, CA as tangents and incentre is the intersection of internal angular bisectors. Whereas the excentre is formed by the external angular bisectors. If we don’t remember formulas, we use this information to proceed through the problem.