Question

If in a quadrilateral, each pair of opposite angles is equal, then it is parallelogram.

Answer 1

Hint: In this theorem we have proof that in a quadrilateral, each pair of opposite angles is parallelogram. For that we are going to prove that it is a parallelogram and has given a step by step solution. A Quadrilateral has four-sides, it is $2$ - dimensional (a flat shape), closed (the lines join up), and has straight sides.

Complete step-by-step answer:
Given that ${\text{ABCD}}$ is a quadrilateral whose opposite angles are equal.

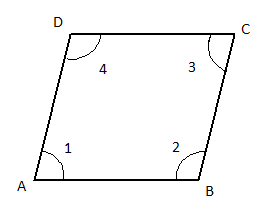
That is, $\angle {\text{A = }}\angle {\text{C}}$ and \[\angle {\text{B = }}\angle {\text{D}}\]
To prove that ${\text{ABCD}}$ is a parallelogram
A parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of measure.
Proof:
As we know the sum of angle of Quadrilateral is ${360^\circ}$
$ \Rightarrow \angle {\text{A + }}\angle {\text{B + }}\angle {\text{C + }}\angle {\text{D = 36}}{{\text{0}}^\circ}$
Since $\angle {\text{A = }}\angle {\text{C}}$ and \[\angle {\text{B = }}\angle {\text{D}}\],
Substitute the terms, we get
$ \Rightarrow \angle {\text{A + }}\angle {\text{D + }}\angle {\text{A + }}\angle {\text{D = 36}}{{\text{0}}^\circ}$
Here adding the terms, we have that
$ \Rightarrow 2\angle {\text{A + 2}}\angle {\text{D = 36}}{{\text{0}}^\circ}$
By taking the value common,
\[ \Rightarrow 2(\angle {\text{A + }}\angle {\text{D) = 36}}{{\text{0}}^\circ}\]
By dividing the term, we get
$ \Rightarrow \angle {\text{A + }}\angle {\text{D = 18}}{{\text{0}}^\circ}$(Co-interior angle)
$ \Rightarrow {\text{AB}}$ is parallelogram to ${\text{DC}}$
Similarly, $\angle {\text{A + }}\angle {\text{B + }}\angle {\text{C + }}\angle {\text{D = 36}}{{\text{0}}^\circ}$
Since $\angle {\text{A = }}\angle {\text{C}}$ and \[\angle {\text{B = }}\angle {\text{D}}\],
Substitute the terms, we get
$ \Rightarrow \angle {\text{A + }}\angle {\text{B + }}\angle {\text{A + }}\angle {\text{B = 36}}{{\text{0}}^\circ}$
Adding the terms, we have that
$ \Rightarrow 2\angle {\text{A + 2}}\angle {\text{B = 36}}{{\text{0}}^\circ}$
By taking the value common,
\[ \Rightarrow 2(\angle {\text{A + }}\angle {\text{B) = 36}}{{\text{0}}^\circ}\]
By dividing the term, we get
$ \Rightarrow \angle {\text{A + }}\angle {\text{B = 18}}{{\text{0}}^\circ}$ (Co-interior angle)
$ \Rightarrow {\text{AB}}$ is parallelogram to ${\text{BC}}$
Hence ${\text{AB}}$ parallelogram to ${\text{DC}}$. And ${\text{AB}}$is parallelogram to ${\text{BC}}$
$\therefore $ ${\text{ABCD}}$ is a parallelogram.

Note: A quadrilateral is a polygon with four sides. There are seven quadrilaterals, some that are surely familiar to you, and some that may not be so familiar. The quadrilateral family tree in the following figure.