Question

If $\hat u$ and $\hat v$ are the unit vectors and $\theta $ is the acute angle between them, then $2\hat u \times 3\hat v$ is a unit vector for
A.Exactly two values of $\theta $
B.More than two values of $\theta $
C.No value of $\theta $
D.Exactly one value of $\theta $

Answer 1

Hint: At first, we will learn about the cross product, and its formula i.e. \[\vec a \times \vec b = \left( {\left| {\vec a} \right|\left| {\vec b} \right|\sin \beta } \right)\hat n\].Using this we will simplify the given expression, from where we will get an equation in $\theta $ or in the function of $\theta $, therefore solving that equation we will get our answer.
We know that the magnitude of the cross product of 2 vectors a and b is given by \[\left| {\vec a \times \vec b} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\sin \theta \] where $\theta $ is the angle between the two vectors. Then we can find the magnitude of the cross product of the given vectors. Then we can equate it to unity and solve for the angle $\theta $. Then the number of solutions of $\theta $ will give the required option.

Complete step-by-step answer:
We are given that $\hat u$ and $\hat v$ are two unit vectors and $\theta $ is the acute angle between them

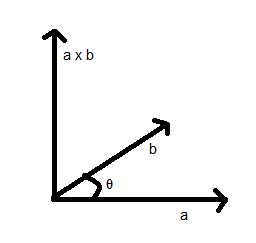
We know that the cross product of two vectors is also a vector perpendicular to both the vectors. We know that the magnitude of the cross product of 2 vectors a and b is given by \[\left| {\vec a \times \vec b} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\sin \theta \] where $\theta $ is the angle between the two vectors.
We are given the vectors $\hat u$ and $\hat v$
We can find the magnitude of $2\hat u \times 3\hat v$.
 $ \Rightarrow \left| {2\hat u \times 3\hat v} \right| = \left| {2\hat u} \right|\left| {3\hat v} \right|\sin \theta $
We know that $\left| {c\vec a} \right| = c\left| {\vec a} \right|$. So, we get,
 $ \Rightarrow \left| {2\hat u \times 3\hat v} \right| = 2\left| {\hat u} \right| \times 3\left| {\hat v} \right| \times \sin \theta $
Since it is given that $\hat u$ and $\hat v$ is the unit vectors i.e. \[\left| {\hat u} \right| = \left| {\hat v} \right| = 1\]. So, we get,
 $ \Rightarrow \left| {2\hat u \times 3\hat v} \right| = 2 \times 3 \times \sin \theta $
On simplification we get,
 $ \Rightarrow \left| {2\hat u \times 3\hat v} \right| = 6\sin \theta $ … (1)
We need to find the angle when the cross product will give a unit vector. For $2\hat u \times 3\hat v$ to be a unit vector, its modulus should be equal to 1.
i.e. $ \Rightarrow \left| {2\hat u \times 3\hat v} \right| = 1$ …. (2)
On equating (1) and (2), we get,
 $ \Rightarrow 1 = 6\sin \theta $
On dividing the equation by 6 we get,
 $ \Rightarrow \sin \theta = \dfrac{1}{6}$
Taking both side expression as a function of ${\sin ^{ - 1}}$
 $ \Rightarrow \theta = {\sin ^{ - 1}}\dfrac{1}{6}$
Therefore $\theta $ has only one value which makes it an acute angle.
Therefore, the correct answer is option D.

Note: While solving the equation for $\theta $ most of the students take the value of $\theta $ as $\theta = {\sin ^{ - 1}}\dfrac{1}{6}$ and $\theta = \pi - {\sin ^{ - 1}}\dfrac{1}{6}$, but it is mentioned the question that the $\theta $ is an acute angle so it cannot take the value $\theta = \pi - {\sin ^{ - 1}}\dfrac{1}{6}$, and will have only one solution, so remember to apply all the given data to get a more accurate answer.
The vector product of two vectors will give another vector. The resultant vector will be perpendicular to both the vectors. It will be zero if the vectors are parallel. The scalar product of two vectors will give a scalar quantity. It will be zero if the vectors are perpendicular to each other.