Question

If $f(x) = x + \dfrac{1}{x}$ , $x > 0$ then its greatest value is
A) -2
B) 0
C) 2
D) None of these

Answer 1

Hint: To find the answer of the question, You have to differentiate a given function with equal to zero. Then find the value of $x$ from the first differentiation. Then do a second differentiation and put a value of $x$ In it and check whether the coming answer is negative or positive. If it’s negative then put that value of $x$ in our main function and you will find the answer.

Complete step by step answer:
Let’s write given function once again,
$ \Rightarrow f(x) = x + \dfrac{1}{x}$
Now, differentiate our function with equal to zero to find the value for $x$ and we will get,
$ \Rightarrow f'(x) = 0$
$ \Rightarrow f'(x) = 1 - \dfrac{1}{{{x^2}}} = 0$
From further simplification we will get,
$ \Rightarrow {x^2} = 1$
Find the value for $x$ and we will get,
$ \Rightarrow x = \pm 1$
But, it’s given that $x > 0$ so just consider positive value of $x$ ,
So, value for $x$ is
$ \Rightarrow x = 1$
Now, do second differentiation,
$ \Rightarrow f''(x) = \dfrac{2}{{{x^3}}}$
Now, put value for $x$ that we find from first differentiation,
$ \Rightarrow f''(1) = \dfrac{2}{{{1^3}}}$
From further simplification we will get,
$ \Rightarrow f''(1) = 2$
See our second differentiation is positive in value so $x$ is minimum at $x=1$
So, it’s clear that we could not find the maximum value for a given equation with condition $x > 0$.
We can see the graph of the given function here for better understanding of the scenario:

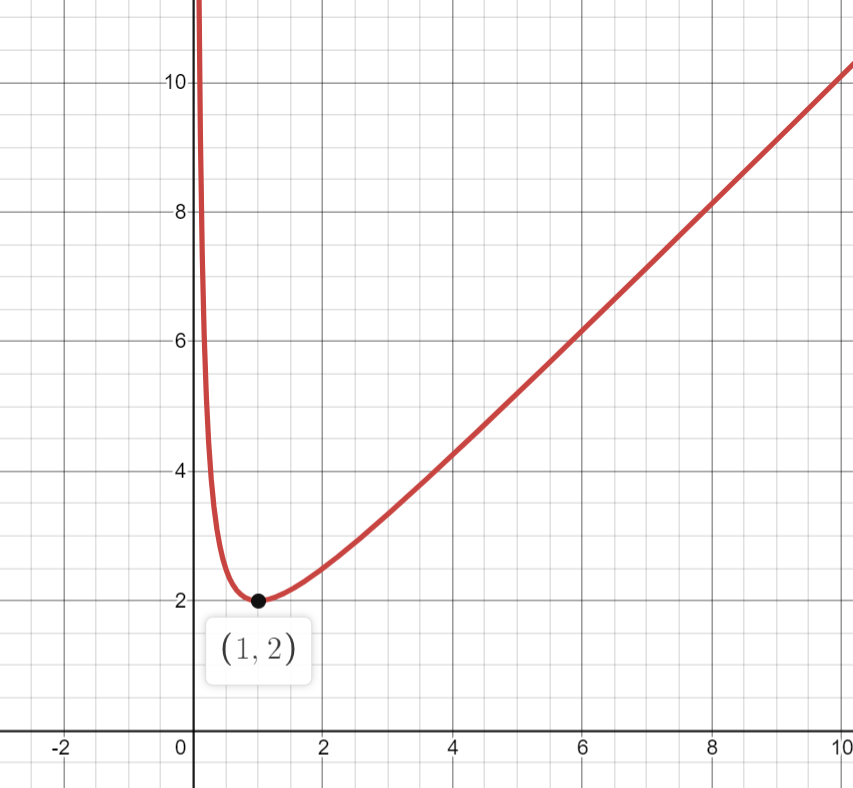
So, the correct answer for this problem is option (D) None of these.

Note:
In this problem we have to find our maximum value, but what if they ask for the minimum value? so there is nothing new for that. You just have to do a second differentiation and check whether the coming value is positive or negative. If value is positive then at that value for $x$ function have minimum value else if value is negative then at That value for $x$ function have greatest value.