Question

If $f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}$ where $\left[ x \right]$ denotes the integral part of $x$ is a periodic function with the period.

Answer 1

Hint:
Hint: For $f(x)$ to be periodic function so we know that a function f is periodic with period T if $f(x + T) = f(x)$ where $T$ is the period. We’ll also use the property of the greatest integer function that is $x - [x] = \{ x\} $ and its period is 1.

Complete step by step solution:
Here we are given the function which is defined as $f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}$ where $\left[ x \right]$ denotes the integral part. We need to find the period of this function. Given that the function is periodic now we need to know what the periodic function means. So periodic function is the function which repeats its value after the regular interval. For example any trigonometric function repeats its value after the interval $2\pi $. Periodic function can be easily determined by using the graph. So for the periodic function it must follow that $f(x + T) = f(x)$ where $T$ represents the period. Now if we are given the function
$f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}$
We need to find the period of the function ${\sin ^3}\pi x$ and $x - [x]$
So let us suppose that $g(x) = x - [x]$
Now if we take $g(x + T) = x + T - [x + T]$
Now we know that $x - [x] = \{ x\} $
Here $\{ x\} $ is the fractional part of $x$ whose graph is given by

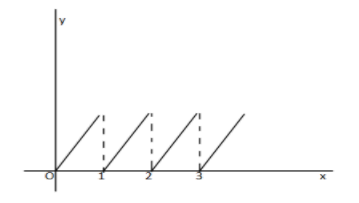
So as we see the graph is similar in $[0,1),[1,2),...{\text{and so on}}$
Hence we can say that $g(x + 1) = g(x)$
Therefore the period of $x - [x] = \{ x\} $ is $1$
For ${\sin ^3}\pi x$ if we replace $x \to x + 2$
Then we can write as ${\sin ^3}\pi (x + 2)$
Which is ${(\sin (2\pi + \pi x))^3}$
And we know that $\sin (2\pi + \theta ) = \sin \theta $
If we take $h(x) = {\sin ^3}\pi x$
$h(x + 2) = {\sin ^3}(2\pi + \pi x)$
 $ = {\sin ^3}\pi x$
$\Rightarrow h(x + 2) = h(x)$
Therefore its period is $2$
Now for finding the period of ${\sin ^3}\pi x + x - [x]$
We need to take the LCM of $1,2$ which is $2$
And as we have the function $f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}$
 ${\sin ^3}\pi x + x - [x]$ has the period $2$
So $f(x)$ has the period $2$
As we can find $f(x + 2)$
$
  f(x + 2) = {2^{{{\sin }^3}\pi (x + 2) + x + 2 - \left[ {x + 2} \right]}} \\
\Rightarrow f(x + 2) = {2^{{{\sin }^3}(2\pi + \pi x) + x + 2 - [x] - 2}} \\
 $
$\Rightarrow f(x + 2) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}$$ = f(x)$

So, the period of $f(x)$ is $2$.

Note:
If $f(x)$ is periodic with the period $T$ then we can write that $f(x + nT) = f(x)$
We can also write that $f(x + 2T) = f(x + T) = f(x)$ and so on
All the trigonometric function have the period $2\pi $
For example for $\sin x$
$f(x + 2\pi ) = \sin (x + 2\pi ) = \sin x = f(x)$
So $2\pi $ is the period.